Đề kiểm tra 15 phút - Đề số 3 - Bài 12 - Chương 1 - Hình học 8Giải Đề kiểm tra 15 phút - Đề số 3 - Bài 12 - Chương 1 - Hình học 8 Quảng cáo
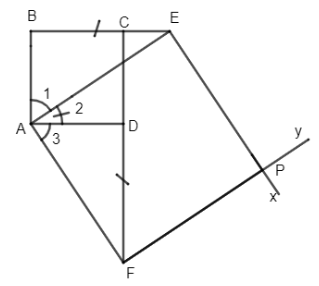
Đề bài Cho hình vuông ABCD, trên tia đối của CB lấy điểm E, trên tia đối của DC lấy điểm F sao cho DF = BE. Qua E kẻ \(Ex// AF\) , qua F kẻ \(Fy// AE.\) Gọi P là giao điểm của Ex và Fy. Chứng minh rằng AEPF là hình vuông. Phương pháp giải - Xem chi tiết Sử dụng: Tứ giác có hai cặp cạnh đối song song là hình bình hành Hình bình hành có một góc vuông và hai cạnh kề bằng nhau là vuông. Lời giải chi tiết Xét hai tam giác ABE và ADF có: AB = AD (gt) BE = DF (giả thiết) \( \Rightarrow \Delta ABE = \Delta ADF\left( {c.g.c} \right)\) \( \Rightarrow \widehat {{A_1}} = \widehat {{A_3}}\) và AE = AF (1) Lại có \(\widehat {{A_1}} + \widehat {{A_2}} = 90^o \Rightarrow \widehat {{A_3}} + \widehat {{A_2}} = 90^o\) (2) Mặt khác do \(EP// AF;EP// AE \Rightarrow AEPF\) là hình bình hành (3) Từ (1), (2) và (3) \( \Rightarrow AEPF\) là hình vuông Loigiaihay.com
|




















Danh sách bình luận