Đề kiểm tra 15 phút - Đề số 2 - Bài 1 - Chương 3 - Hình học 9

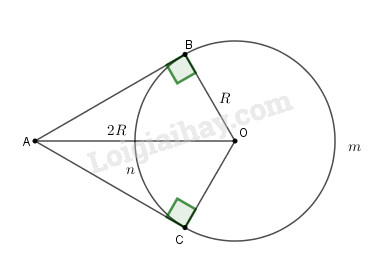
Đề bài

Cho đường tròn (O; R). Một điểm A ở ngoài đường tròn sao cho OA = 2R. Vẽ các tiếp tuyến AB và AC đến (O) ( A , B là hai tiếp điểm).

a) Tính số đo các \(\widehat {AOB}\) và \(\widehat {BOC}\).

b) Tính số đo cung nhỏ và cung lớn BC.

Lời giải chi tiết

a) AB là tiếp tuyến của (O; R) nên AB \(\bot\) OB. 

∆ABO vuông tại B có : OA = 2R,    OB =  R (gt) nên là nửa tam giác đều \(\Rightarrow \widehat {AOB} = 60^\circ \).

Do đó \(\widehat {BOC} = 2\widehat {AOB}\) (tính chất hai tiếp tuyến cắt nhau)

hay      \(\widehat {BOC} = 120^\circ \).

b) Ta có: \(\widehat {BOC} = 120^\circ \) (cmt)

\(\Rightarrow sd\overparen{BnC}=120^o\)

\(\Rightarrow sd\overparen{BmC}=360^o-120^o=240^o\)

 Loigiaihay.com