Đề kiểm tra 15 phút - Đề số 1 - Bài 7 - Chương 3 - Hình học 9

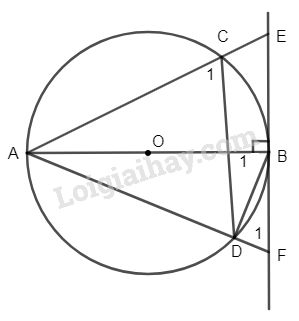
Đề bài

Cho đường tròn (O) đường kính AB. Từ A kẻ hai đường thẳng cắt đường tròn tại C và D, cắt tiếp tuyến của đường tròn vẽ qua B tại E và F.

a) Chứng minh các điểm C, E, F, D cùng thuộc một đường tròn.

b) Chứng minh: \(FB^2= FA.FD\).

Lời giải chi tiết

a) Nối B và D có :

\(\widehat {{C_1}} = \widehat {{B_1}}\) ( góc nội tiếp cùng chắn cung AD)

\(\widehat {{B_1}} = \widehat {{F_1}}\) ( cùng phụ với\(\widehat {DBF}\)),

\( \Rightarrow \widehat {{C_1}} = \widehat {{F_1}}.\)

Do đó tứ giác CEFD nội tiếp hay bốn điểm C, E, F, D cùng thuộc một đường tròn.

Cách giải khác :

\(\widehat F = \dfrac{{sd\overparen{AB} - sd\overparen{BD}} }{2} = \dfrac{{sd\overparen{AD}}}{ 2}\)( góc có đỉnh bên ngoài)

\(\widehat {{C_1}} =\dfrac {{sd\overparen{AD}} }{ 2}\)  ( góc nội tiếp) \( \Rightarrow \widehat F = \widehat {{C_1}}\).

b) \(∆ABF\) vuông ( tính chất tiếp tuyến) có BD là đường cao nên \(FB^2= FA.FD\) ( hệ thức lượng trong tam giác vuông).

Loigiaihay.com