Đề cương ôn tập học kỳ II môn toán lớp 9Tổng hợp kiến thức cần nắm vững, các dạng bài tập và câu hỏi có khả năng xuất hiện trong đề thi HK2 môn toán 9 sắp tới Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
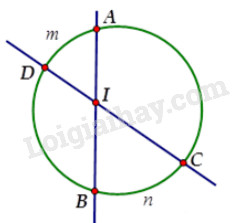
Đại 1. Cách giải hệ phương trình bằng phương pháp thế Để giải hệ phương trình bậc nhất hai ẩn bằng phương pháp thế, ta làm như sau: Bước 1. Rút x hoặc y từ một phương trình của hệ phương trình, thay vào phương trình còn lại, ta được phương trình mới chỉ còn một ẩn. Bước 2. Giải phương trình một ẩn vừa có, rồi từ đó suy ra nghiệm của hệ phương trình đã cho. Chú ý + Nếu thấy xuất hiện phương trình có các hệ số của hai ẩn đểu bằng 0 thì hệ phương trình đã cho có thể có vô số nghiệm hoặc vô nghiệm. 2. Cách giải hệ phương trình bằng phương pháp cộng đại số Bước 1: Nhân các vế của hai phương trình với số thích hợp (nếu cần) sao cho các hệ số của một ẩn nào đó trong hai phương trình của hệ bằng nhau hoặc đối nhau. Bước 2: Sử dụng quy tắc cộng đại số để được hệ phương trình mới, trong đó có một phương trình mà hệ số của một trong hai ẩn bằng 0 (tức là phương trình một ẩn). Bước 3: Giải phương trình một ẩn vừa thu được rồi suy ra nghiệm của hệ đã cho. 3. Cách giải bài toán bằng cách lập hệ hai phương trình bậc nhất hai ẩn Ta làm theo ba bước sau: Bước 1: Lập hệ phương trình - Chọn hai ẩn và đặt điều kiện thích hợp cho chúng - Biểu diễn các đại lượng chưa biết theo các ẩn và các đại lượng đã biết - Lập hai phương trình biểu thị mỗi quan hệ giữa các đại lượng. Bước 2: Giải hệ phương trình nói trên. Bước 3: Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thích hợp với bài toán và kết luận. 4. Hàm số \(y = a{x^2}\) \((a ≠ 0)\) a. Tập xác định của hàm số \(y = a{x^2}\) \((a ≠ 0)\) Hàm số \(y = a{x^2}\) \((a ≠ 0)\) xác định với mọi giá trị của \(x ∈ R.\) nên tập xác định \(D=R.\) b. Tính chất Xét hàm số \(y = a{x^2}\) \((a ≠ 0)\) - Nếu \(a > 0\) thì hàm số nghịch biến khi \(x < 0\) và đồng biến khi \(x > 0\). - Nếu \(a < 0\) thì hàm số đồng biến khi \(x < 0\) và nghịch biến khi \(x > 0\). Nhận xét Xét hàm số \(y = a{x^2}\) \((a ≠ 0)\) - Nếu \(a > 0\) thì \(y > 0\) với mọi \(x ≠ 0; y = 0\) khi \(x = 0\). Giá trị nhỏ nhất của hàm số \(y = 0\). - Nếu \(a < 0\) thì \(y < 0\) với mọi \(x ≠ 0; y = 0\) khi \(x = 0\). Giá trị lớn nhất của hàm số là \(y = 0\). c. Đồ thị hàm số Đồ thị của hàm số \(y = a{x^2}\) (\(a ≠ 0\)) là một đường cong đi qua gốc tọa độ và nhận trục Oy làm trục đối xứng. Đường cong đó được gọi là một parabol với đỉnh O. - Nếu \(a > 0\) thì đồ thị nằm phía trên trục hoành, O là điểm thấp nhất của đồ thị. - Nếu \(a < 0\) thì đồ thị nằm phía dưới trục hoành, O là điểm cao nhất của đồ thị. d. Cách vẽ đồ thị Bước 1: Tìm tập xác định của hàm số. Bước 2: Lập bảng giá trị (thường từ \(5\) đến \(7\) giá trị) tương ứng giữa \(x\) và \(y.\) Bước 3: Vẽ đồ thị và kết luận. 5. Phương trình bậc hai một ẩn a. Định nghĩa Phương trình bậc hai một ẩn là phương trình có dạng: \(a{x^2} + bx + c=0\) Trong đó \(x\) là ẩn số; \(a, b, c\) là những số cho trước gọi là các hệ số và \(a ≠ 0\). b. Công thức nghiệm của phương trình bậc hai Đối với phương trình \(a{x^2} + bx + c = 0(a \ne 0)\) và biệt thức \(\Delta = {b^2} - 4ac\): +) Nếu \(\Delta > 0\) thì phương trình có hai nghiệm phân biệt: \({x_1}\)= \(\dfrac{-b + \sqrt{\bigtriangleup }}{2a}\) và \({x_2}\)= \(\dfrac{-b - \sqrt{\bigtriangleup }}{2a}\) +) Nếu \(\Delta = 0\) thì phương trình có nghiệm kép \({x_1}={x_2}=\dfrac{-b }{2a}\). +) Nếu \(\Delta < 0\) thì phương trình vô nghiệm. Chú ý: Nếu phương trình \(a{x^2} + bx + c = 0\, (a \ne 0)\) có \(a\) và \(c\) trái dấu, tức là \(ac < 0\) thì phương trình có hai nghiệm phân biệt. c. Công thức nghiệm thu gọn Đối với phương trình \(a{x^2} + bx + c = 0\,(a \ne 0)\) và \(b = 2b'\), \(\Delta ' = b{'^2} - ac\) + Nếu \(\Delta ' >0\) thì phương trình có hai nghiệm phân biệt: \({x_1}=\dfrac{-b' + \sqrt{\bigtriangleup '}}{a}\); \({x_2}=\dfrac{-b' - \sqrt{\bigtriangleup '}}{a}\) + Nếu \(\Delta ' =0\) thì phương trình có nghiệm kép \({x_1}={x_2}=\dfrac{-b'}{a}\). + Nếu \(\Delta ' <0\) thì phương trình vô nghiệm. 6. Hệ thức Vi-ét và ứng dụng a. Hệ thức Vi-ét Nếu \({x_1},{\rm{ }}{x_2}\) là hai nghiệm của phương trình \(a{x^2} + bx + c = 0\,(a \ne 0)\) thì: \(\left\{\begin{matrix} x_{1} + x_{2} = -\dfrac{b}{a}& & \\ x_{1}x_{2}=\dfrac{c}{a} & & \end{matrix}\right.\) b. Ứng dụng Tính nhẩm nghiệm +) Nếu phương trình \(a{x^2} + bx + c = 0\,(a \ne 0)\) có \(a + b + c = 0\) thì phương trình có một nghiệm \({x_1}= 1\), còn nghiệm kia là \({x_2}=\dfrac{c}{a}.\) +) Nếu phương trình \(a{x^2} + bx + c = 0\,(a \ne 0)\) có \(a - b + c = 0\) thì phương trình có nghiệm là \({x_1}= -1\), còn nghiệm kia là \({x_2}=\dfrac{-c}{a}\). c. Tìm hai số khi biết tổng và tích của chúng Nếu hai số có tổng bằng \(S\) và tích bằng \(P\) và \({S^2}-{\rm{ }}4P{\rm{ }} \ge {\rm{ }}0\) thì hai số đó là hai nghiệm của phương trình: \({x^2}-{\rm{ }}Sx{\rm{ }} + {\rm{ }}P{\rm{ }} = {\rm{ }}0\). 7. Các dạng toán về điều kiện để phương trình có nghiệm thỏa mãn đề bài Cho phương trình: \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\). Điều kiện để phương trình: - Vô nghiệm: \(\Delta < 0\) (\(\Delta ' < 0\)) - Nghiệm kép: \(\Delta = 0\) (\(\Delta ' = 0\)) - Có 2 nghiệm phân biệt: \(\Delta > 0\) (\(\Delta ' > 0\)) - Có 2 nghiệm cùng dấu: \(\left\{ \begin{array}{l}\Delta \left( {\Delta '} \right) \ge 0\\P = {x_1}.{x_2} > 0\end{array} \right.\) - Có 2 nghiệm cùng dấu âm: \(\left\{ \begin{array}{l}\Delta \left( {\Delta '} \right) \ge 0\\P = {x_1}.{x_2} > 0\\S = {x_1} + {x_2} < 0\end{array} \right.\) - Có 2 nghiệm cùng dấu dương: \(\left\{ \begin{array}{l}\Delta \left( {\Delta '} \right) \ge 0\\P = {x_1}.{x_2} > 0\\S = {x_1} + {x_2} > 0\end{array} \right.\) - Có 2 nghiệm khác dấu: \(\left\{ \begin{array}{l}\Delta \left( {\Delta '} \right) \ge 0\\P = {x_1}.{x_2} < 0\end{array} \right.\) hoặc \(a.c < 0\) 7. Phương trình quy về phương trình bậc hai a. Phương trình trùng phương Định nghĩa: Phương trình trùng phương là phương trình có dạng: \(a{x^4} + {\rm{ }}b{x^2} + {\rm{ }}c{\rm{ }} = {\rm{ }}0{\rm{ }}\left( {a{\rm{ }} \ne {\rm{ }}0} \right)\) Cách giải: Giải phương trình trùng phương \(a{x^4} + {\rm{ }}b{x^2} + {\rm{ }}c{\rm{ }} = {\rm{ }}0{\rm{ }}\left( {a{\rm{ }} \ne {\rm{ }}0} \right)\) + Đặt \({x^2} = {\rm{ }}t,{\rm{ }}t{\rm{ }} \ge {\rm{ }}0\). + Giải phương trình \(a{t^2} + {\rm{ }}bt{\rm{ }} + {\rm{ }}c{\rm{ }} = {\rm{ }}0\). + Với mỗi giá trị tìm được của t (thỏa mãn \( t \ge 0\)), lại giải phương trình \({x^2} = {\rm{ }}t\). b. Phương trình chứa ẩn ở mẫu thức Khi giải phương trình chứa ẩn ở mẫu thức, ta làm như sau: Bước 1: Tìm điều kiện xác định của phương trình. Bước 2: Quy đồng mẫu thức hai vế rồi khử mẫu thức. Bước 3: Giải phương trình vừa nhận được. Bước 4: Trong các giá trị tìm được của ẩn, loại các giá trị không thỏa mãn điều kiện xác định, các giá trị thỏa mãn điều kiện xác định là nghiệm của phương trình đã cho. 8. Các bước giải bài toán bằng cách lập phương trình Bước 1: Lập phương trình - Chọn ẩn và đặt điều kiện thích hợp cho chúng - Biểu diễn các đại lượng chưa biết theo các ẩn và các đại lượng đã biết. - Lập phương trình biểu thị mối quan hệ giữa các đại lượng . Bước 2: Giải phương trình nói trên. Bước 3: Trả lời: Kiểm tra xem trong các nghiệm của phương trình, nghiệm nào thỏa mãn điều kiện và kết luận. Hình 1. Góc ở tâm a. Định nghĩa Góc có đỉnh trùng với tâm đường tròn được gọi là góc ở tâm b. Số đo cung Số đo cung của cung nhỏ bằng số đo của góc ở tâm chắn cung đó. Số đo của cung lớn bằng \(360^0\) trừ đi số đo của cung nhỏ Số đo của nửa đường tròn bằng \(180^0\) c. So sánh hai cung Hai cung được gọi là bằng nhau nếu chúng có số đo bằng nhau Trong hai cung, cung nào có số đo lớn hơn được gọi là cung lớn hơn. Chú ý: Nếu C là một điểm nằm trên cung AB thì: \(sđ\overparen{AB}\) = \(sđ\overparen{AC}\)+ \(sđ\overparen{CB}\) 2. Liên hệ giữa cung và dây Với hai cung nhỏ trong một đường tròn hay hai đường tròn bằng nhau: a) Hai cung bằng nhau căng hai dây bằng nhau b) Hai dây bằng nhau căng hai cung bằng nhau c) Cung lớn hơn căng dây lớn hơn d) Dây lớn hơn căng cung lớn hơn 3. Góc nội tiếp Định nghĩa: - Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó. - Cung nằm bên trong góc nội tiếp được gọi là cung bị chắn. Định lý Trong một đường tròn, số đo của góc nội tiếp bằng nửa số đo của cung bị chắn. Hệ quả Trong một đường tròn: a) Các góc nội tiếp bằng nhau chắn các cung bằng nhau. b) Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau. c) Góc nội tiếp (nhỏ hơn hoặc bằng \(90^\circ \)) có số đo bằng nửa số đo góc ở tâm cùng chắn một cung. d) Góc nội tiếp chắn nửa đường tròn là góc vuông. 4. Góc tạo bởi tia tiếp tuyến và dây cung Định nghĩa: Cho đường tròn tâm \((O)\) có \(Ax\) là tia tiếp tuyến tại tiếp điểm \(A\) và dây cung \(AB.\) Khi đó, góc \(BAx\) là góc tạo bởi tia tiếp tuyến và dây cung. Định lý: Số đo của góc tạo bởi tia tiếp tuyến và dây cung bằng nửa số đo của cung bị chắn. Hệ quả: Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau. 5. Góc có đỉnh bên trong đường tròn, góc có đỉnh bên ngoài đường tròn a. Góc có đỉnh bên trong đường tròn Định nghĩa: Trong hình dưới , góc \(BIC\) nằm trong đường tròn \((O)\) được gọi là góc có đỉnh ở bên trong đường tròn.
Định lý: Số đo của góc đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn. b. Góc có đỉnh bên ngoài đường tròn Định nghĩa: Góc có đỉnh nằm bên ngoài đường tròn và các cạnh đều có điểm chung với đường tròn là góc có đỉnh bên ngoài đường tròn. Định lý: Số đo của góc có đỉnh bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn. 6. Đường tròn ngoại tiếp, đường tròn nội tiếp Định nghĩa Đường tròn đi qua tất cả các đỉnh của một đa giác được gọi là đường tròn ngoại tiếp đa giác và đa giác được gọi là đa giác nội tiếp đường tròn. Đường tròn tiếp xúc với tất cả các cạnh của một đa giác được gọi là đường tròn nội tiếp đa giác và đa giác được gọi là đa giác ngoại tiếp đường tròn. Định lý Bất kì đa giác đều nào cũng có một và chỉ một đường tròn ngoại tiếp, có một và chỉ một đường tròn nội tiếp. 7. Tứ giác nội tiếp Định nghĩa Tứ giác nội tiếp đường tròn là tứ giác có bốn đỉnh nằm trên đường tròn đó. Định lý - Trong một tứ giác nội tiếp, tổng số đo hai góc đối diện bằng \(180^\circ \). - Nếu một tứ giác có tổng số đo hai góc đối diện bằng \(180^\circ \) thì tứ giác đó nội tiếp được đường tròn. Một số dấu hiệu nhận biết tứ giác nội tiếp - Tứ giác có tổng hai góc đối bằng \(180^\circ \). - Tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối với đỉnh đó. - Tứ giác có bốn đỉnh cách đều một điểm ( mà có thể xác định được ). Điểm đó là tâm đường tròn ngoại tiếp tứ giác. - Tứ giác có hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới cùng một góc \(\alpha \). Chú ý : Trong các hình đã học thì hình chữ nhật , hình vuông, hình thang cân nội tiếp được đường tròn. 8. Độ dài đường tròn, cung tròn Công thức tính độ dài đường tròn (chu vi đường tròn) Cho đường tròn \(\left( {O;R} \right)\), độ dài \(\left( C \right)\) của đường tròn ( hay chu vi của đường tròn) là \(C = 2\pi R\,\)hay \(C = \pi d\,\,\)với \(d = 2R\) là đường kính của \(\left( O \right)\) . Công thức tính độ dài cung tròn Trên đường tròn bán kính\(R\) , độ dài \(l\) của một cung \(n^\circ \) được tính theo công thức \(l = \dfrac{{\pi Rn}}{{180}}\,\). 9. Diện tích hình tròn, quạt tròn Công thức tính diện tích hình tròn Diện tích \(S\) của một hình tròn bán kính \(R\) được tính theo công thức \(S = \pi {R^2}\) Công thức tính diện tích hình quạt tròn Diện tích hình quạt tròn bán kính R, cung \(n^\circ \) được tính theo công thức \(S = \dfrac{{\pi {R^2}n}}{{360}}\,\,hay\,\,\,S = \dfrac{{l.{\rm{R}}}}{2}\) ( với \(l\) là độ dài cung \(n^\circ \)của hình quạt tròn). 10. Hình trụ Cho hình trụ có bán kính đáy \(R\) và chiều cao \(h\). Khi đó : + Diện tích xung quanh : \({S_{xq}} = 2\pi Rh\) . + Diện tích 1 đáy : \({S_đ} = \pi {R^2}\). + Diện tích toàn phần : \({S_{tp}} = {S_{xq}} + 2{S_đ} = 2\pi Rh +2 \pi {R^2}.\) + Thể tích : \(V = \pi {R^2}h\). 11. Hình nón Cho hình nón có bán kính đáy \(R\), đường sinh \(l\), chiều cao \(h\). Khi đó : + Diện tích xung quanh: \({S_{xq}} = \pi Rl.\) + Diện tích đáy : \({S_đ} = \pi {R^2}\) + Diện tích toàn phần: \({S_{tp}} = {S_{xq}} + {S_đ} = \pi Rl + \pi {R^2}.\) + Thể tích: \(V = \dfrac{1}{3}\pi {R^2}h.\) + Công thức liên hệ : \({R^2} + {h^2} = {l^2}\) 12. Hình nón cụt Cho hình nón cụt có các bán kính đáy là \(R\) và \(r,\)chiều cao \(h,\) đường sinh \(l.\) + Diện tích xung quanh: \({S_{xq}} = \pi (R + r)l.\) + Diện tích toàn phần: \({S_{tp}} = \pi (R + r)l + \pi {R^2} + \pi {r^2}.\) + Thể tích: \(V = \dfrac{1}{3}\pi h({R^2} + Rr + {r^2}).\) 13. Hình cầu Cho hình cầu bán kính \(R.\) - Diện tích mặt cầu :\(S = 4\pi {R^2}\) . - Thể tích hình cầu : \(V = \dfrac{4}{3}\pi {R^3}\). Loigiaihay.com
|




















Danh sách bình luận