Câu hỏi:
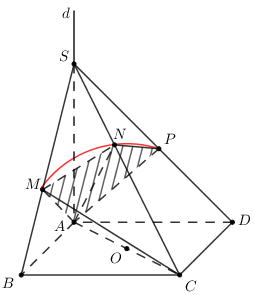
Trong mặt phẳng (P) cho hình vuông ABCD cạnh \(a\). Trên đường thẳng qua A và vuông góc với mặt phẳng (P) lấy điểm S sao cho \(SA = a\). Mặt cầu đường kính AC cắt các đường thẳng SB, SC, SD lần lượt tại \(M \ne B,\,\,N \ne C,\,\,P \ne D\). Tính diện tích tứ giác AMNP?
- A \(\dfrac{{{a^2}\sqrt 6 }}{2}\)
- B \(\dfrac{{{a^2}\sqrt 2 }}{{12}}\)
- C \(\dfrac{{{a^2}\sqrt 2 }}{4}\)
- D \(\dfrac{{{a^2}\sqrt 3 }}{6}\)
Phương pháp giải:
+) Chứng minh \(SC \bot \left( {AMNP} \right)\).
+) Sử dụng công thức tỉ số thể tích tính thể tích chóp S.AMNP.
+) Sử dụng công thức tính thể tích \({V_{S.AMNP}} = \dfrac{1}{3}SN.{S_{AMNP}} \Rightarrow {S_{AMNP}} = \dfrac{{3{V_{S.AMNP}}}}{{SN}}\).
Lời giải chi tiết:
Gọi \(O = AC \cap BD\).
Do M thuộc mặt cầu đường kính AC \( \Rightarrow \widehat {AMC} = {90^0} \Rightarrow MC \bot MA\).
Ta có \(\left\{ \begin{array}{l}BC \bot AB\,\,\left( {gt} \right)\\BC \bot SA\,\,\left( {SA \bot \left( {ABCD} \right)} \right)\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot AM\)
\( \Rightarrow AM \bot \left( {SBC} \right) \Rightarrow AM \bot SB\) và \(AM \bot SC\).
Chứng minh tương tự ta có \(AP \bot \left( {SCD} \right) \Rightarrow AP \bot SC;\,\,AP \bot SD\).
N thuộc mặt cầu đường kính \(AC \Rightarrow \widehat {ANC} = {90^0} \Rightarrow AN \bot SC\).
\( \Rightarrow SC \bot \left( {AMNP} \right)\).
Áp dụng hệ thức lượng trong tam giác vuông SAC ta có \(SN = \dfrac{{S{A^2}}}{{SC}} = \dfrac{{S{A^2}}}{{\sqrt {S{A^2} + A{C^2}} }} = \dfrac{{{a^2}}}{{\sqrt {{a^2} + 2{a^2}} }} = \dfrac{a}{{\sqrt 3 }}\) và \(\dfrac{{SN}}{{SC}} = \dfrac{{S{A^2}}}{{S{C^2}}} = \dfrac{{{a^2}}}{{{a^2} + 2{a^2}}} = \dfrac{1}{3}\).
Áp dụng hệ thức lượng trong tam giác vuông SAB ta có \(\dfrac{{SM}}{{SB}} = \dfrac{{S{A^2}}}{{S{B^2}}} = \dfrac{{{a^2}}}{{{a^2} + {a^2}}} = \dfrac{1}{2}\).
Áp dụng hệ thức lượng trong tam giác vuông SAD ta có \(\dfrac{{SP}}{{SD}} = \dfrac{{S{A^2}}}{{S{D^2}}} = \dfrac{{{a^2}}}{{{a^2} + {a^2}}} = \dfrac{1}{2}\).
Ta có:
\(\begin{array}{l}\dfrac{{{V_{S.AMN}}}}{{{V_{S.ABC}}}} = \dfrac{{SM}}{{SB}}.\dfrac{{SN}}{{SC}} = \dfrac{1}{2}.\dfrac{1}{3} = \dfrac{1}{6} \Rightarrow {V_{S.AMN}} = \dfrac{1}{6}{V_{S.ABC}} = \dfrac{1}{{12}}{V_{S.ABCD}}\\\dfrac{{{V_{S.ANP}}}}{{{V_{S.ACD}}}} = \dfrac{{SN}}{{SC}}.\dfrac{{SP}}{{SD}} = \dfrac{1}{3}.\dfrac{1}{2} = \dfrac{1}{6} \Rightarrow {V_{S.ANP}} = \dfrac{1}{6}{V_{S.ACD}} = \dfrac{1}{{12}}{V_{S.ABCD}}\\ \Rightarrow {V_{S.AMNP}} = {V_{S.AMN}} + {V_{S.ANP}} = \dfrac{1}{{12}}{V_{S.ABCD}} + \dfrac{1}{{12}}{V_{S.ABCD}} = \dfrac{1}{6}{V_{S.ABCD}} = \dfrac{1}{6}.\dfrac{1}{3}.SA.{S_{ABCD}} = \dfrac{{{a^3}}}{{18}}\end{array}\)
Lại có \({V_{S.AMNP}} = \dfrac{1}{3}SN.{S_{AMNP}} \Rightarrow {S_{AMNP}} = \dfrac{{3{V_{S.AMNP}}}}{{SN}} = \dfrac{{3.\dfrac{{{a^3}}}{{18}}}}{{\dfrac{a}{{\sqrt 3 }}}} = \dfrac{{{a^2}\sqrt 3 }}{6}\).
Chọn D.