Câu hỏi:
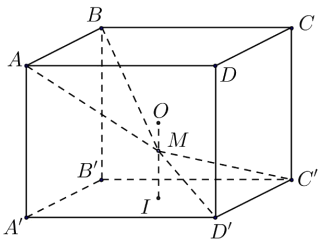
Cho hình lập phương ABCD. A’B’C’D’ có tâm O. Gọi I là tâm của hình vuông A’B’C’D’ và M là điểm thuộc đoạn thẳng OI sao cho \(MO = \frac{1}{2}MI\) (tham khảo hình vẽ). Khi đó cosin của góc tạo bởi hai mặt phẳng (MC’D’) và (MAB) bằng
- A \(\frac{{6\sqrt {13} }}{{65}}.\)
- B \(\frac{{7\sqrt {85} }}{{85}}.\)
- C \(\frac{{6\sqrt {85} }}{{85}}.\)
- D \(\frac{17\sqrt{13}}{65}.\)
Phương pháp giải:
Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và vuông góc với giao tuyến.
Lời giải chi tiết:
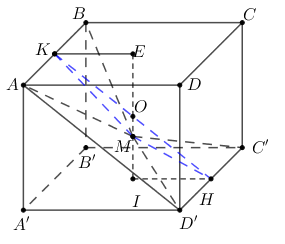
Nhận thấy giao tuyến (d) của hai mặt phẳng \(\left( {MAB} \right),\left( {MC'D'} \right)\) là đường thẳng đi qua \(M\) và song song với \(AB,C'D'\)
Do \(M\in OI\Rightarrow MA=MB\Rightarrow \Delta MAB\) cân tại M, tương tự \(\Delta MC'D'\) cân tại M. Gọi K, H lần lượt là trung điểm của AB và C’D’ ta có:
Do đó \(MK \bot AB \Rightarrow MK \bot d;MH \bot C'D' \Rightarrow MH \bot d\)
Khi đó \(\left( {\left( {MC'D'} \right),\left( {MAB} \right)} \right) = \left( {MH,MK} \right) = \varphi \Rightarrow \cos \varphi = \left| {\cos \widehat {HMK}} \right|\)
Giả sử hình lập phương có cạnh bằng \(6\)
Ta có: \(IM=2,IH=3\Rightarrow MH=\sqrt{13}\)
Gọi \(E\) là tâm hình vuông \(ABCD \Rightarrow EM = 4;EK = 3 \Rightarrow MK = \sqrt {{4^2} + {3^2}} = 5\)
Mà \(HK = AD' = 6\sqrt 2 \)
Suy ra \(\left| {\cos \widehat {HMK}} \right| = \left| {\frac{{M{K^2} + M{H^2} - H{K^2}}}{{2MH.MK}}} \right| = \left| {\frac{{25 + 13 - 72}}{{2.5\sqrt {13} }}} \right| = \left| {\frac{{ - 34}}{{10\sqrt {13} }}} \right| = \frac{{17\sqrt {13} }}{{65}}\)
Vậy \(\cos \varphi =\frac{17\sqrt{13}}{65}\)
Chọn D.


















