Câu hỏi:
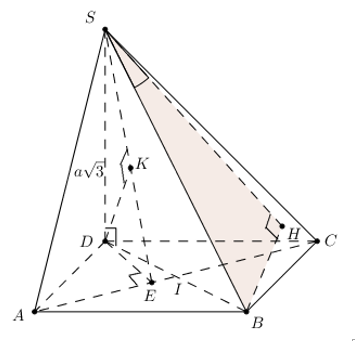
Chóp S.ABCD, ABCD là hình bình hành, AB = 2a, BC = a, \(\widehat{ABC}={{120}^{0}},\,\,SD=a\sqrt{3},\,\,SD\bot \left( ABCD \right)\)Tính \(\widehat{\left( SB;\left( SAC \right) \right)}\) ?
- A \(\arcsin \frac{1}{4}\)
- B \(\arcsin \frac{1}{5}\)
- C \(\arcsin \frac{1}{6}\)
- D \(\arcsin \frac{1}{7}\)
Phương pháp giải:
Lời giải chi tiết:
* \(\Delta ABC\) :
\(\begin{align} A{{C}^{2}}=B{{A}^{2}}+B{{C}^{2}}-2BA.BC.\cos {{120}^{0}} \\ \,\,\,\,\,\,\,\,\,\,\,=4{{a}^{2}}+{{a}^{2}}-2.2a.a.\left( -\frac{1}{2} \right)=7{{a}^{2}}\Rightarrow AC=a\sqrt{7} \\ \end{align}\)\(\begin{align} *\,\,\Delta DCB:\,\,B{{D}^{2}}=C{{D}^{2}}+C{{B}^{2}}-2CD.CD.\cos {{60}^{0}} \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=4{{a}^{2}}+{{a}^{2}}-2.2a.a.\frac{1}{2}=3{{a}^{2}} \\ \Rightarrow BD=a\sqrt{3}\Rightarrow SB=a\sqrt{6} \\ \end{align}\)
* Vẽ \(DE\bot AC\) có
\({{S}_{\Delta ABC}}=\frac{1}{2}a.2a.\sin {{120}^{0}}=\frac{1}{2}DE.AC\Rightarrow DE=\frac{a\sqrt{3}}{\sqrt{7}}\).
* Vẽ giả tưởng \(BH\bot \left( SAC \right)\Rightarrow \widehat{\left( SB;\left( SAC \right) \right)}=\widehat{BSH}\).
* \(BH=d\left( B;\left( SAC \right) \right)=d\left( A;\left( SAC \right) \right)=DK\)
\(\frac{1}{D{{K}^{2}}}=\frac{1}{S{{D}^{2}}}+\frac{1}{D{{E}^{2}}}=\frac{1}{3{{a}^{2}}}+\frac{7}{3{{a}^{2}}}=\frac{8}{3{{a}^{2}}}\Rightarrow DK=\frac{a\sqrt{3}}{2\sqrt{2}}\).
* Tam giác vuông \(SHB:\,\,\sin \widehat{BSH}=\frac{BH}{SB}=\frac{\sqrt{3}}{2\sqrt{2}}:a\sqrt{6}=\frac{1}{4}\)
Chọn đáp án A.