Phương pháp giải:

+) Chứng minh tam giác SHC đều, kẻ $CK \bot SH$, chứng minh $CK//OO'$.

+) $CK//OO' \Rightarrow \angle \left( {OO';\left( {ABC} \right)} \right) = \angle \left( {CK;\left( {ABC} \right)} \right)$.

+) Xác định góc giữa $CK$ và $\left( {ABC} \right)$ và tính góc đó.

Lời giải chi tiết:

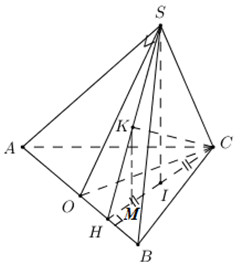
Ta có: $SI \bot \left( {ABC} \right) \Rightarrow SI \bot HC$.

Xét tam giác $SHC$ có $SI$ là trung tuyến đồng thời là đường cao $\Rightarrow \Delta SHC$ cân tại $S \Rightarrow SH = SC\,\,\left( 1 \right)$

Ta có: $\left\{ \begin{array}{l}AB \bot HC\\AB \bot SI\end{array} \right. \Rightarrow AB \bot \left( {SHC} \right) \Rightarrow AB \bot SH$.

Do $\Delta ABC$ vuông tại C và $\Delta SAB$ vuông tại S, lại có $O$ là trung điểm của $AB \Rightarrow OA = OB = OS = OC$.

Xét tam giác vuông $OSH$ và tam giác vuông $OCH$ có:

$OS = OC\,\,\left( {cmt} \right);\,\,OH\,\,chung$

$\Rightarrow \Delta OSH = \Delta OCH$ (cạnh huyền – cạnh góc vuông) $\Rightarrow SH = CH\,\,\left( 2 \right)$

Từ (1) và (2) $\Rightarrow \Delta SHC$ đều.

Gọi $K$ là trung điểm của $SH$ ta có $CK \bot SH$.

Do $AB \bot \left( {SHC} \right)\,\,\left( {cmt} \right) \Rightarrow AB \bot CK \Rightarrow CK \bot \left( {SAB} \right)$ (3).

Vì tam giác $SAB$ vuông tại $S \Rightarrow O$ là tâm đường tròn ngoại tiếp $\Delta SAB$.

$O'$ là tâm mặt cầu ngoại tiếp tứ diện $ABSI \Rightarrow OO'$ là trục của $\Delta SAB \Rightarrow OO' \bot \left( {SAB} \right)$  (4).

Từ (3) và (4) $\Rightarrow CK//OO' \Rightarrow \angle \left( {OO';\left( {ABC} \right)} \right) = \angle \left( {CK;\left( {ABC} \right)} \right)$.

Trong $\left( {SHC} \right)$ kẻ $KM//SI\,\,\left( {M \in CH} \right) \Rightarrow CM$ là hình chiếu của $CK$ trên $\left( {ABC} \right)$.

$\Rightarrow \angle \left( {CK;\left( {ABC} \right)} \right) = \angle \left( {CK;CM} \right) =   \angle KCM = \angle KCH$.

Do tam giác $SHC$ là tam giác đều (cmt) $\Rightarrow$ Đường cao $CK$ đồng thời là phân giác $\Rightarrow \angle KCH = {30^0}$.

Vậy $\angle \left( {OO';\left( {ABC} \right)} \right) = {30^0} \Rightarrow \alpha  = {30^0} \Rightarrow \cos \alpha  = \dfrac{{\sqrt 3 }}{2}$.

Chọn A.