Câu hỏi:
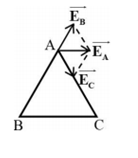
Hai điện tích điểm qB = −qC = 8,1.10-8C, đặt tại 2 đỉnh B và C của một tam giác đều ABC cạnh bằng a = 8cm, trong không khí.
a. Tính độ lớn cường độ điện trường tổng hợp \(\overrightarrow{{{E}_{A}}}\) do qB và qC gây ra tại đỉnh A của tam giác?
b. Xác định góc hợp bởi vec tơ điện trường tổng hợp \(\overrightarrow{{{E}_{A}}}\) với cạnh BC?
- A a) 8100V/m; b) 300
- B a) 8100V/m; b) 600
- C a) 3000V/m; b) 300
- D a) 3000V/m; b) 600
Phương pháp giải:
- Áp dụng công thức tính cường độ điện trường E = k|q|/r2
- Cường độ điện trường tổng hợp được tính theo công thức cộng vec tơ
Lời giải chi tiết:
a)
Cường độ điện trường tổng hợp tại A:
\(\overrightarrow{{{E}_{A}}}=\overrightarrow{{{E}_{C}}}+\overrightarrow{{{E}_{B}}}\)
Do qB = |qC| và rB = rC = a nên \({{E}_{B}}={{E}_{C}}=k\frac{|{{q}_{C}}|}{{{a}^{2}}}=8100V/m\)
Do hình bình hành tạo bởi \(\overrightarrow{{{E}_{B}}},\overrightarrow{{{E}_{C}}}\) là hình thoi và góc tạo bởi hai vec tơ đó là 1200 nên \(\overrightarrow{{{E}_{A}}}\) là đường chéo hình thoi với
EA = 2EB cos600 = 8100V/m
b) Do \(\left( \overrightarrow{{{E}_{B}}},\overrightarrow{{{E}_{A}}} \right)={{60}^{0}}\Rightarrow \overrightarrow{{{E}_{A}}}\) cùng hướng với BC nên góc hợp giữa chúng là 00