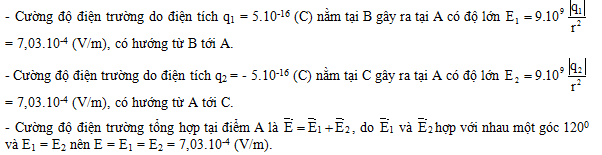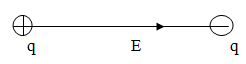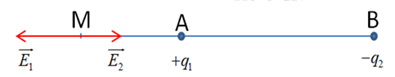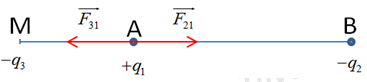50 bài tập Điện trường và cường độ điện trường - đường sức điện mức độ vận dụngLàm bàiQuảng cáo
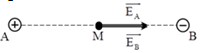
Câu hỏi 1 : Hai điện tích q1 = 5.10-16 (C), q2 = - 5.10-16 (C), đặt tại hai đỉnh B và C của một tam giác đều ABC cạnh bằng 8 (cm) trong không khí. Cường độ điện trường tại đỉnh A của tam giác ABC có độ lớn là:
Đáp án: D Lời giải chi tiết: Câu hỏi 2 : Cho hai điện tích dương q1 = 2 (nC) và q2 = 0,018 (μC) đặt cố định và cách nhau 10 (cm). Đặt thêm điện tích thứ ba q0 tại một điểm trên đường nối hai điện tích q1, q2 sao cho q0 nằm cân bằng. Vị trí của q0 là
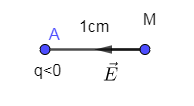
Đáp án: A Lời giải chi tiết: Câu hỏi 3 : Một điện tích điểm dương Q trong chân không gây ra tại điểm M cách điện tích một khoảng r = 30 cm một điện trường có cường độ E = 40000 V/m. Độ lớn điện tích Q là
Đáp án: B Phương pháp giải: Áp dụng công thức tính cường độ điện trường của điện tích điểm gây ra tại một điểm cách điện tích một khoảng r:$$E = {9.10^9}{Q \over {{r^2}}}$$ Lời giải chi tiết: $$E = {9.10^9}{Q \over {{r^2}}} = > Q = {4.10^{ - 7}}C$$ Câu hỏi 4 : Trong không khí, người ta bố trí 2 điện tích có cùng độ lớn 0,5 μC nhưng trái dấu cách nhau 2 m. Tại trung điểm của 2 điện tích, cường độ điện trường là
Đáp án: C Phương pháp giải: Lời giải chi tiết: Đáp án C + Cường độ điện trường tại trung điểm có độ lớn và hướng về điện tích âm. Câu hỏi 5 : Hai tấm kim loại phẳng nhiễm điện trái dấu đặt nằm ngang trong dầu, điện trường giữa hai bản là điện trường đều có vectơ cường độ điện \(\overrightarrow E \) trường hướng từ trên xuống dưới và E = 2.104V/m. Một quả cầu bằng sắt bán kính 1cm mang điện tích q nằm lơ lửng ở khoảng không gian giữa hai tấm kim loại. Biết khối lượng riêng của sắt là 7800kg/m3, của dầu là 800kg/m3, lấy g = 10m/s2, π = 3,14. Giá trị điện tích q gần giá trị nào nhất sau đây ?
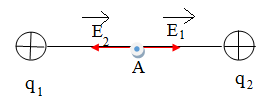
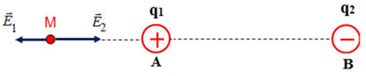
Đáp án: B Phương pháp giải: Phương pháp: Áp dụng điều kiện cân bằng của một vật Lời giải chi tiết: Đáp án B + Để quả cầu cân bằng (nằm lơ lửng) \(\overrightarrow P + \overrightarrow {{F_{a\sin }}} + \overrightarrow {{F_d}} = 0 \Leftrightarrow P = {F_{a\sin }} + {F_d}\) Lực điện hướng lên ngược chiều điện trường điện tích q là âm. + Thay các giá trị vào phương trình trên \({D_s}Vg = {D_d}Vg + \left| q \right|E \Rightarrow \left| q \right| = {{{D_s}Vg - {D_d}Vg} \over E} = \Delta {\rm{D}}{{g{4 \over 3}\pi {r^3}} \over E} = 14,7\,\,\mu C.\) Câu hỏi 6 : Cho hai điện tích điểm cùng độ lớn nhưng trái dấu đặt cố định trên đường thẳng nằm ngang cách nhau 2m trong chân không. Cường độ điện trường tại trung điểm hai điện tích có chiều hướng sang phải và độ lớn là 18kV/m. Điện tích dương nằm phía bên:
Đáp án: D Phương pháp giải: Cường độ điện trường do điện tích điểm gây ra : E = k|q|/r2
Lời giải chi tiết: Chiều của đường sức điện là đi từ điện tích dương sang điện tích âm, nên điện tích dương nằm phía bên trái. Tại trung điểm thì cường độ điện trường bị chồng chập do điện tích dương và điện tích âm gây ra, khoảng cách từ điện tích đên trung điểm là 1m. \(E = {{k.\left| q \right|} \over {{r^2}}} + {{k.\left| q \right|} \over {{r^2}}} = 2.{{k.\left| q \right|} \over {{r^2}}} = 2.k.\left| q \right|\) Thay số từ đề bài: \(\left| q \right| = {E \over {2.k}} = {{{{18.10}^3}} \over {{{2.9.10}^9}}} = {1.10^{ - 6}} = 1\mu C\) Câu hỏi 7 : Hai điện tích điểm q1 = 20nC và q2 = -20nC đặt tại hai điểm A,B cách nhau một đoạn a = 30cm trong không khí. Cho k = 9.109Nm2/C2. Cường độ điện trường tại điểm M cách đều A và B một khoảng bằng a có độ lớn là
Đáp án: C Phương pháp giải: Sử dụng nguyên lí chồng chất điện trường Lời giải chi tiết: Từ hình vẽ suy ra: \({E_M} = 2{E_{1M}}\cos {60^0} = {E_{1M}} = {{k{q_1}} \over {{a^2}}}\) Câu hỏi 8 : Tại 3 đỉnh của tam giác ABC vuông tại A cạnh BC =50cm ;AC =40cm ;AB =30cm ta đặt các điện tích Q1 = Q2 = Q3 = 10-9C .Xác định cường độ điện trường tại H với H là chân đường cao kẻ từ
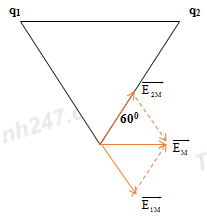
Đáp án: B Phương pháp giải: áp dụng công thức tính cảm ứng điện trường \(E = {{k\left| Q \right|} \over {r_{}^2}}\) Lời giải chi tiết: Đáp án B + Áp dụng hệ thức lượng trong tam giác vuông, ta có: HC = 32 cm, HB = 18 cm, AH = 24 cm. + Cường độ điện trường do các điện tích gây ra tại H có chiều như hình vẽ và có độ lớn lần lượt là:
\(\eqalign{ + Cường độ điện trường tổng hợp tại H: \({E_H} = \sqrt {E_A^2 + {{\left( {{E_B} - {E_C}} \right)}^2}} \approx 246\,V/m\) Câu hỏi 9 : Hai điện tích q1 = +q và q2 = -q và đặt tại A và B trong không khí, biết AB = 2a. Tại M trên đường trung trực của AB thì EM có giá trị cực đại. Giá trị cực đại đó là
Đáp án: C Phương pháp giải: Lời giải chi tiết: Đáp án C + Dễ thấy rằng cường độ điện trường tổng hợp lớn nhất tại trung điểm của AB. + Ta có \({E_M} = 2{{kq} \over {{a^2}}}.\) Câu hỏi 10 : Một giọt dầu nằm lơ lửng trong điện trường của một tụ điện phẳng. Đường kính của giọt dầu là 0,4mm. Khối lượng riêng của dầu là 800kg/m3. Hiệu điện thế và khoảng cách giữa hai bản lần lượt là 100 V và 1cm. Bản tụ phía trên mang điện tích âm. Bỏ qua lực đẩy Ác-si-mét. Lấy g = 10m/s2. Điện tích của giọt dầu là
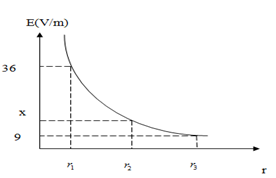
Đáp án: A Phương pháp giải: Sử dụng điều kiện cân bằng của vật chịu tác dụng của hai lực, công thức tính lực điện trường. Lời giải chi tiết: Các lực tác dụng vào giọt dầu: Trọng lực \(\overrightarrow P \) , lực điện trường \(\overrightarrow F \) Vì giọt dầu nằm lơ lửng trong điện trường nên \(\overrightarrow P + \overrightarrow F = \overrightarrow 0 \Rightarrow \overrightarrow F = - \overrightarrow P \) Suy ra + \(\overrightarrow F \uparrow \downarrow \overrightarrow P \) mà \(\overrightarrow P \uparrow \downarrow \overrightarrow E \) vì bản âm của tụ điện ở phía trên \( \Rightarrow \overrightarrow F \uparrow \uparrow \overrightarrow E \Rightarrow q > 0\) + Về độ lớn \(F = P \Leftrightarrow \left| q \right|E = mg \Leftrightarrow \left| q \right| = {{D.{4 \over 3}\pi {R^3}.g.d} \over U} = {{800.{4 \over 3}\pi .{{\left( {0,{{2.10}^{ - 3}}} \right)}^3}.10.0,01} \over {100}} = 2,{68.10^{ - 11}}C = 26,8pC\) Vậy q = 26,8 pC Chọn A Câu hỏi 11 : Cường độ điện trường của một điện tích phụ thuộc vào khoảng cách r được mô tả như đồ thị bên. Biết 2r2 = r1 + r3 và các điểm cùng nằm trên một đường sức. Giá trị của x bằng
Đáp án: C Phương pháp giải: Sử dụng công thức tính độ lớn điện trường E Lời giải chi tiết: Đáp án C Áp dụng công thức tính điện trường: \(\begin{array}{l}E = \frac{{k.q}}{{{r^2}}} \Rightarrow \frac{{{E_3}}}{{{E_1}}} = \frac{{r_1^2}}{{r_3^2}} = \frac{9}{{36}} = \frac{1}{4} \Rightarrow {r_3} = 2{r_1}\\{r_2} = \frac{{{r_1} + {r_2}}}{2} = \frac{3}{2}{r_1} \Rightarrow {E_2} = \frac{{k.q}}{{{r_2}}} = \frac{{{E_1}.{r_1}^2}}{{{{(1,5{r_1})}^2}}} = 16V/m\end{array}\)
Câu hỏi 12 : Tại một điểm M trong không khí có hai cường độ điện trường có phương vuông góc với nhau và có độ lớn lần lượt là E1 = 6.104 V/m; E2 = 8.104 V/m. Tính cường độ điện trường tổng hợp tại M
Đáp án: A Phương pháp giải: Lời giải chi tiết: Đáp án A Vì 2 vecto cường độ điện trường vuông góc với nhau nên vecto cường độ điện trường tổng hợp được xác định bởi biểu thức \(E = \sqrt {E_1^2 + E_2^2} = \sqrt {{{\left( {{{6.10}^4}} \right)}^2} + {{\left( {{{8.10}^4}} \right)}^2}} = {10.10^4}\) Câu hỏi 13 : Một điện tích điểm q được đặt trong môi trường điện môi. Tại điểm M cách q là 40 cm, điện trường có cường độ 9.105V/m và có chiều hướng về điện tích q. Biết hằng số điện môi của môi trường là 2,5. Điện tích q có giá trị bằng
Đáp án: B Phương pháp giải: Áp dụng công thức tính cường độ điện trường \(E = k\frac{Q}{{\varepsilon {r^2}}}\) Lời giải chi tiết: Đáp án B Độ lớn điện tích q được xác định bởi biểu thức \(\left| q \right| = \frac{{E\varepsilon {r^2}}}{k} = \frac{{{{9.10}^5}.2,5.0,{4^2}}}{{{{9.10}^9}}} = 40\mu C\). Mặt khác vecto cường độ điện trường có chiều hướng về điện tích q nên điện tích q có giá trị là -40μC Câu hỏi 14 : Hai điện tích điểm qB = −qC = 8,1.10-8C, đặt tại 2 đỉnh B và C của một tam giác đều ABC cạnh bằng a = 8cm, trong không khí. a. Tính độ lớn cường độ điện trường tổng hợp \(\overrightarrow{{{E}_{A}}}\) do qB và qC gây ra tại đỉnh A của tam giác? b. Xác định góc hợp bởi vec tơ điện trường tổng hợp \(\overrightarrow{{{E}_{A}}}\) với cạnh BC?
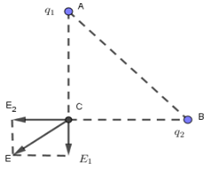
Đáp án: B Phương pháp giải: - Áp dụng công thức tính cường độ điện trường E = k|q|/r2 - Cường độ điện trường tổng hợp được tính theo công thức cộng vec tơ Lời giải chi tiết: a) Cường độ điện trường tổng hợp tại A: \(\overrightarrow{{{E}_{A}}}=\overrightarrow{{{E}_{C}}}+\overrightarrow{{{E}_{B}}}\) Do qB = |qC| và rB = rC = a nên \({{E}_{B}}={{E}_{C}}=k\frac{|{{q}_{C}}|}{{{a}^{2}}}=8100V/m\) Do hình bình hành tạo bởi \(\overrightarrow{{{E}_{B}}},\overrightarrow{{{E}_{C}}}\) là hình thoi và góc tạo bởi hai vec tơ đó là 1200 nên \(\overrightarrow{{{E}_{A}}}\) là đường chéo hình thoi với EA = 2EB cos600 = 8100V/m b) Do \(\left( \overrightarrow{{{E}_{B}}},\overrightarrow{{{E}_{A}}} \right)={{60}^{0}}\Rightarrow \overrightarrow{{{E}_{A}}}\) cùng hướng với BC nên góc hợp giữa chúng là 00 Câu hỏi 15 : Cho hai điện tích q1 = 8.10–8C và q2 = –1,6.10–7C đặt tại hai điểm A và B cách nhau một khoảng AB = 4cm trong không khí. a) Tính độ lớn lực tương tác điện giữa hai điện tích ? b) Điểm M cách A, B những đoạn : AM = 2cm, BM = 6cm. Vẽ và tính độ lớn cường độ điện trường tổng hợp tại điểm M.
Đáp án: A Phương pháp giải: - Lực tương tác tính điện: \(F=\frac{k\left| {{q}_{1}}{{q}_{2}} \right|}{{{r}^{2}}}\) - Cường độ điện trường do điện tích q gây ra tại một điểm cách nó một đoạn r là: \(E=\frac{k\left| q \right|}{{{r}^{2}}}\) - Vecto cường độ điện trường hướng ra xa nếu q> 0; hướng lại gần nếu q < 0. - Cường độ điện trường tại M là tổng hợp cường độ điện trường do hai điện tích q1, q2 gây ra tại M Lời giải chi tiết: a) Độ lớn lực tương tác tĩnh điện giữa hai điện tích: \(F=\frac{k\left| {{q}_{1}}{{q}_{2}} \right|}{{{r}^{2}}}=\frac{{{9.10}^{9}}{{.8.10}^{-8}}{{.1,6.10}^{-7}}}{{{0,04}^{2}}}=0,072N\) b) Cường độ điện trường tại M: \(\overrightarrow{{{E}_{M}}}=\overrightarrow{{{E}_{1}}}+\overrightarrow{{{E}_{2}}}\) Vì q1, q2 trái dấu nên hai vec tơ \(\overrightarrow{{{E}_{1}}};\overrightarrow{{{E}_{2}}}\) trái dấu. Vậy \({{E}_{M}}=\left| {{E}_{1}}-{{E}_{2}} \right|=\left| \frac{k\left| {{q}_{1}} \right|}{A{{M}^{2}}}+\frac{k\left| {{q}_{2}} \right|}{B{{M}^{2}}} \right|=\left| \frac{{{9.10}^{9}}\left| {{8.10}^{-8}} \right|}{{{0,02}^{2}}}+\frac{{{9.10}^{9}}\left| -{{1,6.10}^{-7}} \right|}{{{0,06}^{2}}} \right|\) = 2,2.106V/m Câu hỏi 16 : Hai điện tích q1 = q2 = 5.10–16 C, đặt tại hai đỉnh B và C của một tam giác đều ABC cạnh bằng 8 cm trong không khí. Cường độ điện trường tại đỉnh A có độ lớn là
Đáp án: A Phương pháp giải: Cường độ điện trường do điện tích điểm gây ra tại điểm cách nó đoạn r là \(E=k\frac{\left| q \right|}{{{r}^{2}}}\) Cường độ điệnt rường hướng ra xa điện tích nếu điện tích dương, hướng lại gần điện tích nếu điện tích âm. Lời giải chi tiết: Cường độ điện trường do q1 và q2 gây ra tại A là \({{E}_{B}}={{E}_{C}}=\frac{k{{q}_{1}}}{{{0,08}^{2}}}\) =7,03125.10-4 V/m Cường độ điện trường tổng hợp tại A là \(\overrightarrow{{{E}_{A}}}=\overrightarrow{{{E}_{B}}}+\overrightarrow{{{E}_{C}}}\) Về độ lớn \({{E}_{A}}=\sqrt{E_{B}^{2}+E_{C}^{2}+2{{E}_{B}}{{E}_{C}}\text{cos60}}\) = 1,2178.10-3V/m Chọn A Câu hỏi 17 : Đặt tại hai đỉnh A và B của một tam giác vuông cân ABC (AC = BC = 30cm) lần lượt các điện tích điểm q1 = 3.10-7C và q2. Cho biết hệ thống đặt trong không khí và cường độ điện trường tổng hợp tại đỉnh C có giá trị E = 5.104 V/m. Điện tích q2 có độ lớn
Đáp án: A Phương pháp giải: Cường độ điện trường do điện tích điểm gây ra tại điểm cách nó đoạn r \(E=\frac{k\left| q \right|}{{{r}^{2}}}\) Vec tơ cường độ điện trường hướng ra xa nếu điện tích dương, hướng lại gần nếu điện tích âm. Lời giải chi tiết: Cường độ điện trường tại C là tổng hợp cường độ điện trường do hai điện tích đặt tại A và B gây ra. \(\overrightarrow{E}=\overrightarrow{{{E}_{1}}}+\overrightarrow{E{}_{2}}\) Do tam giác ABC vuông tại C nên \(E=\sqrt{E_{1}^{2}+E_{2}^{2}}=\sqrt{{{\left( \frac{k{{q}_{1}}}{A{{C}^{2}}} \right)}^{2}}+{{\left( \frac{k\left| {{q}_{2}} \right|}{B{{C}^{2}}} \right)}^{2}}}={{5.10}^{4}}V/m\Rightarrow \left| {{q}_{2}} \right|={{4.10}^{-7}}C\) Chọn A Câu hỏi 18 : Tại 2 điểm A, B cách nhau 10 cm trong không khí, đặt 2 điện tích q1 = q2 = - 6.10-6 C. Xác định lực điện trường do hai điện tích này tác dụng lên điện tích q3 = -3.10-8 C đặt tại C. Biết AC = BC = 15 cm.
Đáp án: C Phương pháp giải: Phương pháp: + Áp dụng biểu thức tính lực tương tác tĩnh điện: \(F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\) + Phương pháp tổng hợp lực Lời giải chi tiết: Các điện tích q1 và q2 tác dụng lên điện tích q3 các lực \(\overrightarrow{{{F}_{1}}}\) và \(\overrightarrow{{{F}_{2}}}\) có phương chiều như hình vẽ, có độ lớn: \({{F}_{1}}={{F}_{2}}={{9.10}^{9}}\frac{\left| {{q}_{1}}{{q}_{3}} \right|}{A{{C}^{2}}}={{72.10}^{-3}}N.\) Lực tổng hợp do q1 và q2 tác dụng lên q3 là: \(\overrightarrow{F}=\overrightarrow{{{F}_{1}}}+\overrightarrow{{{F}_{2}}}\); có phương chiều như hình vẽ, có độ lớn: \(F={{F}_{1}}cosa+\text{ }{{F}_{2}}cosa=2{{F}_{1}}cosa=2.{{F}_{1}}.\frac{\sqrt{A{{C}^{2}}-A{{H}^{2}}}}{AC}\approx {{136.10}^{-3}}N.\) Chọn C Câu hỏi 19 : Cho hai điểm A và B cùng nằm trên một đường sức của điện trường do một điện tích điểm đặt tại điểm O gây ra. Biết độ lớn của cường độ điện trường tại A là 36V/m, tại B là 9V/m. Cường độ điện trường tại điểm M có khoảng cách OM thỏa mãn \(\frac{2}{O{{M}^{2}}}=\frac{1}{O{{A}^{2}}}+\frac{1}{O{{B}^{2}}}\) có giá trị là
Đáp án: D Phương pháp giải: Cường độ điện trường do điện tích q gây ra tại điểm cách nó đoạn d trong không khí là \(E=\frac{kq}{{{r}^{2}}}\) Lời giải chi tiết: Ta có: \({{E}_{A}}=\frac{kq}{O{{A}^{2}}}=36V/m\) \({{E}_{B}}=\frac{kq}{O{{B}^{2}}}=9V/m\) Tại M: \({{E}_{M}}=\frac{kq}{O{{M}^{2}}}=\frac{kq}{2O{{A}^{2}}}+\frac{kq}{2O{{B}^{2}}}=\frac{36+9}{2}=22,5V/m\) Chọn D Câu hỏi 20 : Một điện tích điểm q đặt trong không khí, độ lớn cường độ điện trường do điện tích q gây ra tại điểm M cách điện tích 1m là 100V/m. Cường độ điện trường do điện tích này gây ra tại điểm N cách điện tích 2m có độ lớn là
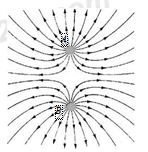
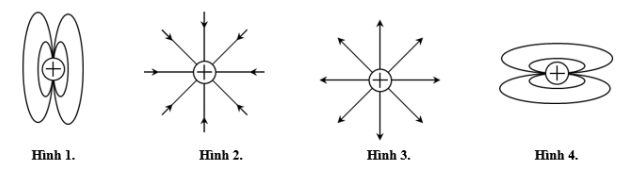
Đáp án: C Phương pháp giải: Cường độ điện trường do điện tích điểm có độ lớn q gây ra tại điểm cách nó đoạn r có độ lớn : \(E=\frac{kq}{\varepsilon {{r}^{2}}}\) Lời giải chi tiết: Cường độ điện trường tại M : \({{E}_{M}}=\frac{kq}{\varepsilon .O{{M}^{2}}}=\frac{kq}{\varepsilon }=100V/m\) Cường độ điện trường tại N là : \({{E}_{N}}=\frac{kq}{\varepsilon .O{{N}^{2}}}=\frac{kq}{4\varepsilon }=\frac{{{E}_{M}}}{4}=25V/m\) Chọn C Câu hỏi 21 : Hình bên có vẽ một số đường sức điện của điện trường do hệ hai điện tích điểm A và B gây ra, đầu các điện tích là
Đáp án: A Phương pháp giải: Phương pháp: Đặc điểm của đường sức điện: Đường sức điện của điện trường tĩnh là đường cong không khép kín. Nó đi ra từ điện tích dương và kết thúc ở điện tích âm. Trong trường hợp chỉ có một điện tích thì các đường sức đi từ điện tích dương ra vô cực hoặc từ vô cực đến điện tích âm Lời giải chi tiết: Hình bên có vẽ một số đường sức điện của điện trường do hệ hai điện tích điểm A và B gây ra. Từ hình vẽ ta có A và B đều tích điện dương Chọn A Câu hỏi 22 : Một điện tích điểm q được đặt trong điện môi đồng tính có hằng số điện môi là \(\text{ }\!\!\varepsilon\!\!\text{ = 2,5}\). Tại một điểm M cách q một đoạn 40 cm, điện trường có cường độ 9.105 V/m và hướng về phía điện tích q. Xác định q?
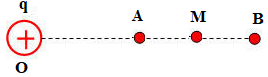
Đáp án: B Phương pháp giải: Cường độ điện trường do q gây ra tại điểm M cách q một đoạn r trong điện môi có: Điểm đặt: Tại M. Phương: đường nối M và q Chiều: hướng ra xa q nếu q >0, hướng vào nếu q <0 Độ lớn: \(\text{E = }\frac{\text{k}\left| \text{q} \right|}{\text{ }\!\!\varepsilon\!\!\text{ }\text{.}{{\text{r}}^{\text{2}}}}\) với k = 9.109 Lời giải chi tiết: Ta có: \(\text{E = }\frac{\text{k}\left| \text{q} \right|}{\text{ }\!\!\varepsilon\!\!\text{ }\text{.}{{\text{r}}^{\text{2}}}}\Rightarrow \left| \text{q} \right|\text{= 40 ( }\!\!\mu\!\!\text{ C)}\) và điện trường hướng về phía q nên q < 0 Câu hỏi 23 : Một điện tích điểm q đặt tại điểm O thì sinh ra điện trường tại điểm A với cường độ điện trường có độ lớn 4000 V/m. Cường độ điện trường tại điểm B là trung điểm của đoạn OA có độ lớn là
Đáp án: D Phương pháp giải: Phương pháp: Công thức tính cường độ điện trường: \(E = k\frac{{\left| q \right|}}{{{r^2}}}\) Lời giải chi tiết: Cách giải: Ta có cường độ điện trường do điện tích điểm q gây ra tại A và tại B là: \(\left\{ \begin{array}{l}{E_A} = k\frac{{\left| q \right|}}{{O{A^2}}}\\{E_B} = k\frac{{\left| q \right|}}{{O{B^2}}}\\OA = 2.OB\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{E_A} = k\frac{{\left| q \right|}}{{4.O{B^2}}}\\{E_B} = k\frac{{\left| q \right|}}{{O{B^2}}}\end{array} \right. \Rightarrow {E_B} = 4.{E_A} = 4.4000 = 16000V/m\) Chọn D Câu hỏi 24 : Một điện tích điểm Q = +4.10-8 C đặt tại một điểm O trong không khí. Cường độ điện trường tại điểm M, cách O một khoảng 2 cm do Q gây ra là
Đáp án: B Phương pháp giải: Công thức tính cường độ điện trường : \(E=\frac{k\left| Q \right|}{\varepsilon {{r}^{2}}}.\) Lời giải chi tiết: Cường độ điện trường tại M do Q gây ra là \(E=\frac{k\left| Q \right|}{\varepsilon {{r}^{2}}}={{9.10}^{5}}(V/m)~~~\) Chọn B Câu hỏi 25 : Lần lượt đặt hai điện tích thử q1, q2 (q1 = 2q2) vào hai điểm A và B trong điện trường. Độ lớn lực điện tác dụng lên q1, q2 lần lượt là F1 và F2, với F1 = 5F2. Độ lớn cường độ điện trường tại A và B là E1 và E2 thỏa mãn
Đáp án: B Phương pháp giải: Công thức tính lực điện: \(F=E.q\) Lời giải chi tiết: \({{F}_{1}}=\left| {{q}_{1}} \right|{{E}_{1}}=\left| 2{{q}_{2}} \right|{{E}_{1}};{{F}_{2}}=\left| {{q}_{2}} \right|{{E}_{2}}\xrightarrow{{{F}_{1}}=5{{F}_{2}}}\left| 2{{q}_{2}} \right|{{E}_{1}}=5\left| {{q}_{2}} \right|{{E}_{2}}\to \)\({{E}_{2}}=0,4{{E}_{1}}\)
Chọn B Câu hỏi 26 : Một điện tích điểm dương Q trong chân không gây ra một điện trường có cường độ \(E = {3.10^4}V/m\)tại điểm M cách điện tích một khoảng 30cm. Tính độ lớn điện tích Q?
Đáp án: D Phương pháp giải: Độ lớn của cường độ điện trường gây ra bởi điện tích Q: \(E = \dfrac{{k\left| Q \right|}}{{{r^2}}} \Rightarrow \left| Q \right|\) Lời giải chi tiết: Ta có: \(E = \dfrac{{k\left| Q \right|}}{{{r^2}}} \Rightarrow \left| Q \right| = \dfrac{{E.{r^2}}}{k} = \dfrac{{{{3.10}^4}.0,{3^2}}}{{{{9.10}^9}}} = {3.10^{ - 7}}C\) Chọn D. Câu hỏi 27 : Trong không khí, người ta bố trí 2 điện tích có cùng độ lớn 0,5 μC cùng dấu cách nhau 2 m. Tại trung điểm của 2 điện tích, cường độ điện trường là
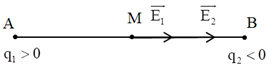
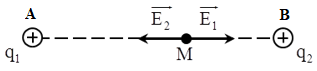
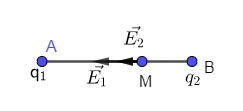
Đáp án: D Phương pháp giải: Áp dụng công thức tính cường độ điện trường \(E = k.\frac{{\left| q \right|}}{{{r^2}}}\) Vẽ hình biểu điễn vecto cường độ điện trường và áp dụng nguyên lí chồng chất điện trường : \(\overrightarrow E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + ...\) Lời giải chi tiết: Vẽ hình biểu điễn vecto cường độ điện trường. Áp dụng nguyên lý chồng chất điện trường : \(\overrightarrow E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} \) Từ hình vẽ ta có : \(\overrightarrow {{E_1}} \uparrow \downarrow \overrightarrow {{E_2}} \Rightarrow E = \left| {{E_1} - {E_2}} \right| = \left| {k.\frac{{{q_1}}}{{{r^2}}} - k.\frac{{{q_2}}}{{{r^2}}}} \right| = 0\) Chọn D. Câu hỏi 28 : Hai điện tích điểm \({q_1} = {2.10^{ - 6}}C\) và \({q_2} = - {8.10^{ - 6}}\)C lần lượt đặt tại hai điểm A và B với AB = 10cm. Gọi \({\overrightarrow E _1}\) và \({\overrightarrow E _2}\) lần lượt là cường độ điện trường do \({q_1}\) và \({q_2}\) sinh ra tại điểm M trên đường thẳng AB. Biết \({\overrightarrow E _2} = 4{\overrightarrow E _1}\)Khẳng định nào sau đây về vị trí điểm M là đúng?
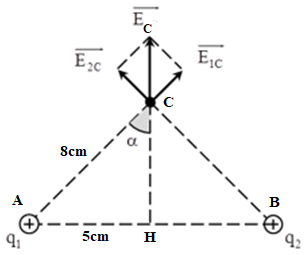
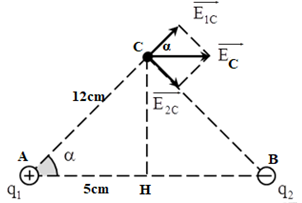
Đáp án: A Phương pháp giải: Cường độ điện trường: \(E = k\dfrac{q}{{{r^2}}}\) Lời giải chi tiết: Ta có: \(\overrightarrow {{E_2}} = 4\overrightarrow {{E_1}} \Rightarrow \overrightarrow {{E_2}} \uparrow \uparrow \overrightarrow {{E_1}} \to \) điểm M nằm trong AB. Xét độ lớn cường độ điện trường tại M, ta có: \(\begin{array}{l}{E_2} = 4{E_1} \Rightarrow k\dfrac{{\left| {{q_2}} \right|}}{{B{M^2}}} = 4k\dfrac{{\left| {{q_1}} \right|}}{{A{M^2}}} \Rightarrow \dfrac{{\left| {{q_2}} \right|}}{{B{M^2}}} = 4\dfrac{{\left| {{q_1}} \right|}}{{A{M^2}}}\\ \Rightarrow \dfrac{{A{M^2}}}{{B{M^2}}} = \dfrac{{4\left| {{q_1}} \right|}}{{\left| {{q_2}} \right|}} = \dfrac{{{{4.2.10}^{ - 6}}}}{{{{8.10}^{ - 6}}}} = 1 \Rightarrow AM = BM\end{array}\) → M là trung điểm của AB \( \Rightarrow AM = BM = \dfrac{{AB}}{2} = \dfrac{{10}}{2} = 5\,\,\left( {cm} \right)\) Chọn A. Câu hỏi 29 : Tại hai điểm A và B cách nhau \(10cm\) trong không khí có đặt hai điện tích \(q_1 = q_2 = 16.10^{ - 8}C.\) Xác định cường độ điện trường do hai điện tích điểm này gây ra tại C biết \(AC = BC = 8cm.\)
Đáp án: A Phương pháp giải: Công thức tính cường độ điện trường: \(E = k.\dfrac{{\left| q \right|}}{{{r^2}}}\) Vẽ hình biểu điễn vecto cường độ điện trường và áp dụng nguyên lí chồng chất điện trường :\(\vec E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + ... + \overrightarrow {{E_n}} \) Lời giải chi tiết: Ta có \(AC = BC = 8 cm\) và \(AB = 10 cm\) nên C nằm trên đường trung trực của AB. Cường độ điện trường tổng hợp tại C: \({\vec E_C} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} {\rm{ }}\) Ta có: \({E_1} = {E_2} = \dfrac{{k.\left| {{q_1}} \right|}}{{A{C^2}}} = \dfrac{{{{9.10}^9}{{.16.10}^{ - 8}}}}{{0,{{08}^2}}} = 2,{25.10^5}V/m\) Từ hình vẽ ta có: \(E_C = 2E_1\cos \alpha = 2E_1.\dfrac{\sqrt{AC^2 - AH^2}}{AC}\) \(\Rightarrow E_C = 2.2,25.10^5.\dfrac{\sqrt{8^2 - 5^2}}{8} = 3,51.10^5\,\,\left ( V/m \right )\) Chọn A. Câu hỏi 30 : Hai điện tích \(q_1 = 1nC\,;\,\,q_2 = - 8nC\) lần lượt đặt tại hai điểm A và B với \(AB = 30cm.\) Xác định điểm M trên đường thẳng AB mà tại đó \(\overrightarrow {{E_2}} = 2\overrightarrow {{E_1}} \)?
Đáp án: D Phương pháp giải: - Công thức tính cường độ điện trường: \(E = k.\dfrac{{\left| q \right|}}{{{r^2}}}\) - Để hai vecto cùng chiều/ngược chiều: + Nếu \({q_1};{q_2}\) cùng dấu, M nằm trong AB thì \(\overrightarrow {{E_1}} \uparrow \downarrow \overrightarrow {{E_2}} \) + Nếu \({q_1};{q_2}\) cùng dấu, M nằm ngoài AB thì \(\overrightarrow {{E_1}} \uparrow \uparrow \overrightarrow {{E_2}} \) + Nếu \({q_1};{q_2}\) trái dấu, M nằm trong AB thì \(\overrightarrow {{E_1}} \uparrow \uparrow \overrightarrow {{E_2}} \) + Nếu \({q_1};{q_2}\) trái dấu, M nằm ngoài AB thì \(\overrightarrow {{E_1}} \uparrow \downarrow \overrightarrow {{E_2}} \) Lời giải chi tiết: Ta có: \(\overrightarrow {{E_2}} = 2\overrightarrow {{E_1}} \Rightarrow \left\{ \begin{array}{l}\overrightarrow {{E_2}} \, \uparrow \uparrow \,\overrightarrow {{E_1}} \,\,\left( 1 \right)\\{E_2} = 2{E_1}\,\,\left( 2 \right)\end{array} \right.\) Vì \({q_1};{q_2}\) trái dấu và kết hợp với \(\overrightarrow {{E_1}} \uparrow \uparrow \overrightarrow {{E_2}} \Rightarrow \) M nằm trong AB \( \Rightarrow AM + BM = AB = 30cm\,\,\left( 3 \right)\) Giải (2) ta có: \(\begin{array}{l}\dfrac{{k\left| {{q_2}} \right|}}{{B{M^2}}} = 2.\dfrac{{k\left| {{q_1}} \right|}}{{A{M^2}}} \Rightarrow \dfrac{{B{M^2}}}{{A{M^2}}} = \dfrac{1}{2}.\dfrac{{\left| {{q_2}} \right|}}{{\left| {{q_1}} \right|}} = 4\\ \Rightarrow BM = 2.AM\,\,\left( 4 \right)\end{array}\) Kết hợp (3) và (4) \( \Rightarrow \left\{ \begin{array}{l}AM = 10cm\\BM = 20cm\end{array} \right.\) Chọn D. Câu hỏi 31 : Tính cường độ điện trường do một điện tích điểm \(Q = + {4.10^{ - 9}}\,\,C\) gây ra tại một điểm cách nó \(5\,\,cm\) trong chân không
Đáp án: B Phương pháp giải: Cường độ điện trường do điện tích điểm gây ra: \(E = k\dfrac{{\left| q \right|}}{{{r^2}}}\) Lời giải chi tiết: Cường độ điện trường tại điểm cách điện tích \(5\,\,cm\) là: \(E = k\dfrac{{\left| q \right|}}{{{r^2}}} = {9.10^9}.\dfrac{{{{4.10}^{ - 9}}}}{{0,{{05}^2}}} = 14400\,\,\left( {V/m} \right) = 14,4\,\,\left( {kV/m} \right)\) Chọn B. Câu hỏi 32 : Cường độ điện trường do một điện tích điểm sinh ra tại A và B nằm trên cùng một đường sức lần lượt là \(49V/m\) và \(25V/m.\) Cường độ điện trường \(E_M\) do điện tích nói trên sinh ra tại điểm M (M là trung điểm của đoạn AB) có giá trị bằng:
Đáp án: A Phương pháp giải: Công thức tính cường độ điện trường: \(E = \dfrac{{k\left| q \right|}}{{{r^2}}}\) Lời giải chi tiết: Biểu diễn các điểm trên hình vẽ: Ta có: \(\left\{ \begin{array}{l}{E_A} = \dfrac{{k\left| q \right|}}{{O{A^2}}} = 49V/m\\{E_B} = \dfrac{{k\left| q \right|}}{{O{B^2}}} = 25V/m\\{E_M} = \dfrac{{k\left| q \right|}}{{O{M^2}}}\end{array} \right.\) M là trung điểm của AB nên: \(OM = \dfrac{{OA + OB}}{2}\) Lấy \(\dfrac{{{E_A}}}{{{E_B}}} = \dfrac{{O{B^2}}}{{O{A^2}}} = \dfrac{{49}}{{25}} \Rightarrow OB = 1,4.OA \Rightarrow OM = 1,2.OA\) Lấy \(\dfrac{{{E_A}}}{{{E_M}}} = \dfrac{{O{M^2}}}{{O{A^2}}} = 1,{2^2} \Rightarrow {E_M} = \dfrac{{{E_A}}}{{1,{2^2}}} = \dfrac{{49}}{{1,{2^2}}} = 34,03V/m\) Chọn A. Câu hỏi 33 : Hình vẽ nào sau đây là đúng khi vẽ đường sức điện của một điện tích dương?
Đáp án: D Phương pháp giải: Lời giải chi tiết: Đáp án D + Đường sức điện của điện tích dương xuất phát từ điện tích dương và kết thúc ở vô cùng. Câu hỏi 34 : Cho hai điện tích điểm nằm dọc theo trục Ox, trong đó điện tích \(q_1 = - 9.10^{ - 6}C\) đặt tại gốc tọa độ O và điện tích \(q_2 = 4.10^{ - 6}C\) nằm cách gốc tọa độ \(20cm.\) Tọa độ của điểm trên trục Ox mà cường độ điện trường tại đó bằng không là
Đáp án: D Phương pháp giải: + Công thức tính cường độ điện trường: \(E = k.\dfrac{{\left| q \right|}}{{{r^2}}}\) + Điện trường tổng hợp tại M: \(\overrightarrow {{E_M}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + ... + \overrightarrow {{E_n}} \) + Điện trường tại M triệt tiêu khi: \(\overrightarrow {{E_M}} = 0\) * Trường hợp: \(\overrightarrow {{E_M}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} = 0 \Rightarrow \left\{ \begin{array}{l}\overrightarrow {{E_1}} \uparrow \downarrow \overrightarrow {{E_2}} \,\,\left( 1 \right)\\{E_1} = {E_2}\,\,\,\,\,\left( 2 \right)\end{array} \right.\) - Nếu \({q_1};{q_2}\) cùng dấu, để \(\overrightarrow {{E_1}} \uparrow \downarrow \overrightarrow {{E_2}} \) thì M nằm trong \({q_1};{q_2}\) - Nếu \({q_1};{q_2}\) trái dấu, để \(\overrightarrow {{E_1}} \uparrow \downarrow \overrightarrow {{E_2}} \) thì M nằm ngoài \({q_1};{q_2}\) Và M nằm gần điện tích có độ lớn nhỏ hơn. Lời giải chi tiết: Giả sử \({q_1}\) đặt tại O và \({q_2}\) đặt tại A. Điện trường tại điểm M sinh ra bởi \({q_1} < 0\) có độ lớn là: \({E_1} = k.\dfrac{{\left| {{q_1}} \right|}}{{O{M^2}}}\) Điện trường tại điểm M sinh ra bởi \({q_2} > 0\) có độ lớn là: \({E_2} = k.\dfrac{{\left| {{q_2}} \right|}}{{M{A^2}}}\) Cường độ điện trường tổng hợp tại M: \(\overrightarrow {{E_M}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} = 0 \Rightarrow \left\{ \begin{array}{l}\overrightarrow {{E_1}} \uparrow \downarrow \overrightarrow {{E_2}} \,\,\left( 1 \right)\\{E_1} = {E_2}\,\,\,\,\,\left( 2 \right)\end{array} \right.\) Từ (1) và (2) ta có hệ phương trình: \(\left\{ \begin{array}{l}OM - AM = OA\\\dfrac{{O{M^2}}}{{A{M^2}}} = \dfrac{{\left| {{q_1}} \right|}}{{\left| {{q_2}} \right|}} = \dfrac{9}{4}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}OM - AM = 20cm\\\dfrac{{OM}}{{AM}} = \dfrac{3}{2}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}OM = 60cm\\AM = 40cm\end{array} \right.\) Chọn D. Câu hỏi 35 : Cho hai điện tích điểm có cùng dấu và độ lớn \(q_1=4q_2\) đặt tại A, B cách nhau \(12 cm.\) Tìm điểm tại đó cường độ điện trường tổng hợp bằng không.
Đáp án: B Phương pháp giải: + Công thức tính cường độ điện trường: \(E = k.\dfrac{{\left| q \right|}}{{{r^2}}}\) + Điện trường tổng hợp tại M: \(\overrightarrow {{E_M}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + ... + \overrightarrow {{E_n}} \) + Điện trường tại M triệt tiêu khi: \(\overrightarrow {{E_M}} = 0\) * Trường hợp: \(\overrightarrow {{E_M}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} = 0 \Rightarrow \left\{ \begin{array}{l}\overrightarrow {{E_1}} \uparrow \downarrow \overrightarrow {{E_2}} \,\,\left( 1 \right)\\{E_1} = {E_2}\,\,\,\,\,\left( 2 \right)\end{array} \right.\) - Nếu \({q_1};{q_2}\) cùng dấu, để \(\overrightarrow {{E_1}} \uparrow \downarrow \overrightarrow {{E_2}} \) thì M nằm trong \({q_1};{q_2}\) - Nếu \({q_1};{q_2}\) trái dấu, để \(\overrightarrow {{E_1}} \uparrow \downarrow \overrightarrow {{E_2}} \) thì M nằm ngoài \({q_1};{q_2}\) Lời giải chi tiết: Gọi M là điểm để cường độ điện trường triệt tiêu, khi đó: \(\overrightarrow {{E_M}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} = 0 \Rightarrow \left\{ \begin{array}{l}\overrightarrow {{E_1}} \uparrow \downarrow \overrightarrow {{E_2}} \,\,\left( 1 \right)\\{E_1} = {E_2}\,\,\,\,\,\left( 2 \right)\end{array} \right.\) Từ (1) và (2) ta có hệ phương trình: \(\left\{ \begin{array}{l}AM + BM = AB\\\dfrac{{A{M^2}}}{{B{M^2}}} = \dfrac{{\left| {{q_1}} \right|}}{{{q_2}}} = 4\end{array} \right. \Rightarrow \left\{ \begin{array}{l}AM + BM = 12cm\\\dfrac{{AM}}{{BM}} = 2\end{array} \right. \Rightarrow \left\{ \begin{array}{l}AM = 8cm\\BM = 4cm\end{array} \right.\) Chọn B. Câu hỏi 36 : Đặt tại hai đỉnh A và B của một tam giác vuông cân ABC (AC = BC = 90cm) lần lượt các điện tích điểm \({q_1} = 5,{4.10^{ - 6}}C\)và \(q_2.\) Cho biết hệ thống đặt trong không khí và cường độ điện trường tổng hợp tại đỉnh C có giá trị \(E = {10.10^4}V/m\). Điện tích \(q_2\) có độ lớn là
Đáp án: C Phương pháp giải: Công thức tính cường độ điện trường: \(E = k.\dfrac{{\left| q \right|}}{{{r^2}}}\) Vẽ hình biểu điễn vecto cường độ điện trường, áp dụng định lí hàm số cos và nguyên lí chồng chất điện trường :\(\vec E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + ... + \overrightarrow {{E_n}} \) Lời giải chi tiết: Ta có: \(\overrightarrow {{E_C}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} \) Vì AC vuông góc với BC \( \Rightarrow \overrightarrow {{E_1}} \bot \overrightarrow {{E_2}} \) Giả sử \({q_2} > 0\) ta có cường độ điện trường tại C được biểu diễn như hình vẽ: Do \(\overrightarrow {{E_1}} \bot \overrightarrow {{E_2}} \Rightarrow {E_C} = \sqrt {E_1^2 + E_2^2} \Rightarrow {E_2} = \sqrt {E_C^2 - E_1^2} \) Mà: \(\left\{ \begin{array}{l}{E_C} = {10.10^4}V/m\\{E_1} = \dfrac{{k\left| {{q_1}} \right|}}{{A{C^2}}} = \dfrac{{{{9.10}^9}.5,{{4.10}^{ - 6}}}}{{0,{9^2}}} = {6.10^4}V/m\end{array} \right.\) \( \Rightarrow {E_2} = \sqrt {E_C^2 - E_1^2} = {8.10^4}V/m\) Lại có: \({E_2} = \dfrac{{k.\left| {{q_2}} \right|}}{{B{C^2}}} \Rightarrow \left| {{q_2}} \right| = \dfrac{{{E_2}.B{C^2}}}{k} = \dfrac{{{{8.10}^4}.0,{9^2}}}{{{{9.10}^9}}} = 7,{2.10^{ - 6}}C\) Chọn C. Câu hỏi 37 : Tại hai điểm A và B cách nhau \(10cm\) trong không khí có đặt 2 điện tích \(q_1 = - q_2 = 6.10^{ - 6}C.\) Xác định cường độ điện trường do hai điện tích điểm này gây ra tại điểm C, biết \(AC = BC = 12 cm.\)
Đáp án: A Phương pháp giải: Công thức tính cường độ điện trường: \(E = k.\dfrac{{\left| q \right|}}{{{r^2}}}\) Vẽ hình biểu điễn vecto cường độ điện trường và áp dụng nguyên lí chồng chất điện trường :\(\vec E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + ... + \overrightarrow {{E_n}} \) Lời giải chi tiết: Ta có \(AC = BC = 12 cm\) và \(AB = 10 cm\) nên C nằm trên trung trực của AB. Cường độ điện trường tổng hợp tại C: \({\vec E_C} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} {\rm{ }}\) Ta có: \({E_1} = {E_2} = \dfrac{{k.\left| {{q_1}} \right|}}{{A{C^2}}} = \dfrac{{{{9.10}^9}{{.6.10}^{ - 6}}}}{{0,{{12}^2}}} = 3,{75.10^6}V/m\) Từ hình vẽ ta có: \(E_C = 2E_1\cos \alpha = 2.3,75.10^6.\dfrac{5}{12} = 3,125.10^6\,\,\left ( V/m \right )\) Chọn A. Câu hỏi 38 : Cho hai điện tích điểm \({q_1} = {6.10^{ - 7}}C;{q_2} = - {8.10^{ - 7}}C\) đặt tại hai điểm A và B trong không khí cách nhau \(5cm.\) Xác định véc tơ cường độ điện trường tổng hợp tại M do \({q_1}\) và \({q_2}\) gây ra tại M biết \(MA = 3cm, MB = 8cm.\)
Đáp án: B Phương pháp giải: Công thức tính cường độ điện trường: \(E = k.\dfrac{{\left| q \right|}}{{{r^2}}}\) Vẽ hình biểu điễn vecto cường độ điện trường và áp dụng nguyên lí chồng chất điện trường: \(\vec E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + ... + \overrightarrow {{E_n}} \) Lời giải chi tiết: + Cường độ điện trường do điện tích \({q_1}\) gây ra tại M: \({E_1} = k\dfrac{{\left| {{q_1}} \right|}}{{A{M^2}}} = {9.10^9}\dfrac{{\left| {{{6.10}^{ - 7}}} \right|}}{{0,{{03}^2}}} = {60.10^5}V/m\) + Cường độ điện trường do điện tích \({q_2}\) gây ra tại M: \({E_2} = k\dfrac{{\left| {{q_2}} \right|}}{{B{M^2}}} = {9.10^9}\dfrac{{\left| { - {{8.10}^{ - 7}}} \right|}}{{0,{{08}^2}}} = 11,{25.10^5}V/m\) Cường độ điện trường tổng hợp tại M: \(\vec E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} {\rm{ }}\) Từ hình vẽ ta có: \(\overrightarrow {{E_1}} \uparrow \downarrow \overrightarrow {{E_2}} \Rightarrow E = \left| {{E_1} - {E_2}} \right|\) \( \Rightarrow E = \left| {{{60.10}^5} - 11,{{25.10}^5}} \right| = 48,{75.10^5}V/m\) Chọn B. Câu hỏi 39 : Cường độ điện trường do một điện tích điểm sinh ra tại A và B nằm trên cùng một đường sức lần lượt là \(25V/m\) và \(49V/m.\) Cường độ điện trường \(E_M\) do điện tích nói trên sinh ra tại điểm M (M là trung điểm của đoạn AB) có giá trị bằng:
Đáp án: A Phương pháp giải: Áp dụng công thức tính cường độ điện trường: \(E = k.\dfrac{{\left| q \right|}}{{{r^2}}}\) Vì điểm M là trung điểm của A và B nên: \({r_M} = \dfrac{{{r_A} + {r_B}}}{2}\) Lời giải chi tiết: Áp dụng công thức tính cường độ điện trường ta xác định được cường độ điện trường tại A, B, M như sau : \(\left\{ {\begin{array}{*{20}{l}}{{E_A} = k.\dfrac{{\left| q \right|}}{{{r_A}^2}} \Rightarrow {r_A} = \sqrt {\dfrac{{k.\left| q \right|}}{{{E_A}}}} }\\{{E_B} = k.\dfrac{{\left| q \right|}}{{{r_B}^2}} \Rightarrow {r_B} = \sqrt {\dfrac{{k.\left| q \right|}}{{{E_B}}}} }\\{{E_M} = k.\dfrac{{\left| q \right|}}{{{r_M}^2}}}\end{array}} \right.\) Vì điểm M là trung điểm của A và B nên: \({r_M} = \dfrac{{{r_A} + {r_B}}}{2}\) Ta có : \(\begin{array}{l}{E_M} = k.\dfrac{{\left| q \right|}}{{{{\left( {\dfrac{{{r_A} + {r_B}}}{2}} \right)}^2}}} = 4k.\dfrac{{\left| q \right|}}{{{{\left( {{r_A} + {r_B}} \right)}^2}}}\\\,\,\,\,\,\,\,\,\, = 4k.\dfrac{{\left| q \right|}}{{{{\left( {\sqrt {\dfrac{{kq}}{{{E_A}}}} + \sqrt {\dfrac{{kq}}{{{E_B}}}} } \right)}^2}}} = \dfrac{4}{{{{\left( {\dfrac{1}{{\sqrt {{E_A}} }} + \dfrac{1}{{\sqrt {{E_B}} }}} \right)}^2}}}\\ \Rightarrow {E_M} = \dfrac{4}{{{{\left( {\dfrac{1}{{\sqrt {25} }} + \dfrac{1}{{\sqrt {49} }}} \right)}^2}}} = \dfrac{{{{4.35}^2}}}{{{{12}^2}}} = 34,02(V/m)\end{array}\) Chọn A. Câu hỏi 40 : Một điện tích q = 5nC đặt tại điểm A. Xác định cường độ điện trường của q tại điểm B cách A một khoảng 10cm:
Đáp án: B Phương pháp giải: Cường độ điện trường: \(E = \dfrac{{k.\left| q \right|}}{{{r^2}}}\) Lời giải chi tiết: Cường độ điện trường tại điểm B cách A một khoảng 10cm là: \(E = \dfrac{{k.\left| q \right|}}{{{r^2}}} = \dfrac{{{{9.10}^9}{{.5.10}^{ - 9}}}}{{0,{1^2}}} = 4500V/m\) Chọn B. Câu hỏi 41 : Trong chân không, tại hai điểm A và B cách nhau 9 cm lần lượt đặt hai điện tích điểm q1 = 4q2 = 4 mC. Chỉ xét tác dụng của lực điện trường, cần đặt điện tích q3 tại điểm C ở đâu để nó nằm cân bằng?
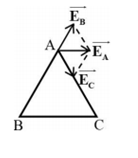
Đáp án: D Phương pháp giải: Áp dụng quy tắc tổng hợp lực Lời giải chi tiết: Đáp án D. + Để diện tích nằm cân bằng thì hợp lực tác dụng lên nó phải bằng hai lực thành phần do q1 tác dụng lên q3 và q2 tác dụng lên q3 phải cùng phương, ngược chiều và cùng dộ lớn. Để F13 và F23 cùng phương, ngược chiều thì q3 phải nằm trên AB và ở giữa AB. + Vì \({\rm{F}} \sim {1 \over {{{\rm{r}}^2}}} \to \) để F13 = F23 thì \({{\rm{r}}_{12}} = 2{{\rm{r}}_{23}} \to {\rm{AC = 6 cm }}\) và BC = 3cm Câu hỏi 42 : Ba điện tích q1, q2, q3 đặt trong không khí lần lượt tại các đỉnh A, B, C của hình vuông ABCD. Biết véc tơ cường độ điện trường tổng hợp tại D có giá là cạnh AD. Quan hệ giữa các điện tích trên là
Đáp án: D Phương pháp giải: Lời giải chi tiết: Đáp án D + Điện trường do gây ra tại D luôn có giá AD => để điện trường tổng hợp do ba điện tích gây ra tại D có hướng AD thì q2 và q3 phải trái dấu. Về mặt độ lớn:\({{\left| {{q_2}} \right|} \over {B{{\rm{D}}^2}}}\cos 45^\circ = {{\left| {{q_1}} \right|} \over {C{D^2}}} \to {q_2} = - 2\sqrt 2 {q_3}\)
Câu hỏi 43 : Một điện tích điểm \(q = {2.10^{ - 7}}C\) đặt tại O trong chân không. Hằng số \(k = {9.10^9}N.{m^2}.k{g^{ - 2}}\). Cường độ điện trường do điện tích điểm gây ra tại M cách O một đoạn 20 cm có độ lớn bằng
Đáp án: B Phương pháp giải: Cường độ điện trường do điện tích Q gây ra tại M cách Q một khoảng r là \(E = k.\frac{{\left| Q \right|}}{{{r^2}}}\) Lời giải chi tiết: Cường độ điện trường do điện tích Q gây ra tại M cách Q một khoảng r là: \(E = k.\frac{{\left| Q \right|}}{{{r^2}}} = {9.10^9}.\frac{{{{2.10}^{ - 7}}}}{{0,{2^2}}} = 45000(V/m) = 45{\rm{ }}\left( {kV/m} \right)\) Chọn B. Câu hỏi 44 : Một điện tích \(q = 1\mu C\) đặt trong điện trường của một điện tích điểm \(Q,\) chịu tác dụng của lực \(F = 0,02N,\) biết rằng hai điện tích đặt cách nhau một khoảng \(r = 18cm.\) Cường độ điện trường \(E\) tại điểm đặt điện tích \(q\) là bao nhiêu ?
Đáp án: C Phương pháp giải: + Vận dụng biểu thức: \(E = \dfrac{F}{q}\) Lời giải chi tiết: Ta có: Cường độ điện trường \(E = \dfrac{F}{q} = \dfrac{{0,02}}{{{{10}^{ - 6}}}} = 20000V/m\) Chọn C Câu hỏi 45 : Cho hai điểm A và B cùng nằm trên một đường sức của điện trường do một điện tích điểm tạo O gây ra. Biết cường độ điện trường tại A là 36V/m và tại B là 16V/m. Cường độ điện trường tại điểm M là trung điểm của AB có giá trị gần nhất với giá trị nào sau đây?
Đáp án: D Phương pháp giải: Áp dụng công thức tính cường độ điện trường do điện tích điểm gây ra tại 1 điểm cách nó 1 khoảng r :\(E = k\frac{q}{{{r^2}}}\) Lời giải chi tiết: Từ công thức xác định cường độ điện tường ta có \(E = k\frac{Q}{{{r^2}}} \to r = \sqrt {\frac{{kQ}}{E}} \) Vì M là trung điểm của AB do đó \({r_M} = \frac{{{r_A} + {r_B}}}{2} \to \sqrt {\frac{{kQ}}{{{E_M}}}} = \frac{{\sqrt {\frac{{kQ}}{{{E_A}}}} + \sqrt {\frac{{kQ}}{{{E_B}}}} }}{2} \to {E_M} = 22,5V/m\) Chọn D Câu hỏi 46 : Xét điểm M nằm trong điện trường của điện tích điểm Q và cách điện tích một khoảng R. Khi dịch m ra xa điện tích Q thêm một đoạn bằng 3R thì cường độ điện trường giảm một lượng 3.105 V/m. Điện trường tại điểm M ban đầu bằng
Đáp án: B Phương pháp giải: Áp dụng công thức tính cường độ điện trường tại 1 điểm $E=k\frac{|Q|}{\varepsilon .{{r}^{2}}}$ Lời giải chi tiết: + Cường độ điện trường tại một điểm $E\sim \frac{1}{{{r}^{2}}}=>E'=\frac{E}{14}$ → Ta có $\Delta E=\frac{15E}{16}=3,2V/m$ . Đáp án B Câu hỏi 47 : Điện tích điểm q đặt tại O trong không khí, Ox là một đường sức điện. Lấy hai điểm A, B trên Ox, M là trung điểm của AB. Độ lớn cường độ điện trường EA, EB, EM có mối liên hệ:
Đáp án: B Phương pháp giải: Áp dụng công thức tính cường độ điện trường do điện tích điểm gây ra và công thức trung điểm trong toán học. Lời giải chi tiết: Cường độ điện trường do điện tích điểm gây ra tại một điểm được tính theo công thức \(E = {{k\left| Q \right|} \over {\varepsilon {r^2}}} \Rightarrow r = \sqrt {{{k\left| Q \right|} \over {E\varepsilon }}} \) Do đó ta tính được rA, rB, rC như sau \({r_A} = \sqrt {{{k\left| Q \right|} \over {{E_A}\varepsilon }}} ;{r_B} = \sqrt {{{k\left| Q \right|} \over {{E_B}\varepsilon }}} ;{r_M} = \sqrt {{{k\left| Q \right|} \over {{E_M}\varepsilon }}} \) Vì M là trung điểm của AB nên ta có \({r_M} = {1 \over 2}\left( {{r_A} + {r_B}} \right) \Leftrightarrow \sqrt {{{k\left| Q \right|} \over {{E_M}\varepsilon }}} = {1 \over 2}\left( {\sqrt {{{k\left| Q \right|} \over {{E_A}\varepsilon }}} + \sqrt {{{k\left| Q \right|} \over {{E_B}\varepsilon }}} } \right) \Leftrightarrow {1 \over {\sqrt {{E_M}} }} = {1 \over 2}\left( {{1 \over {\sqrt {{E_A}} }} + {1 \over {{E_B}}}} \right)\) Chọn đáp án B Câu hỏi 48 : Cho điện tích \({q_1} = - {4.10^{ - 6}}C\) đặt tại A a) Xác định vectơ cường độ điện trường tại M cách A 1 cm trong không khí( Vẽ hình) b) Tại B cách A một khoảng 30 cm trong không khí đặt điện tích \({q_2} = {36.10^{ - 6}}C\) . Xác định cường độ điện trường tại điểm M biết MA = 20 cm, MB = 10cm Phương pháp giải: Áp dụng công thức tính cường độ điện trường tại 1 điểm \(E = k\frac{{\left| q \right|}}{{{r^2}}}\) Nguyên lý chồng chất điện trường Lời giải chi tiết: a. Điện tích đặt tại A là điện tích âm nên vectơ cường độ điện trường đặt tại M cách A 1 cm được xác định như hình dưới b. Cường độ dòng điện tại M do hai điện tích tác dụng được biểu diễn như hình dười Độ lớn cường độ điện trường do \({q_1},{q_2}\) gây ra tại M là \(\begin{array}{l}{E_1} = k\frac{{\left| {{q_1}} \right|}}{{{r^2}}} = {9.10^9}\frac{{\left| { - {{4.10}^{ - 6}}} \right|}}{{{{0,2}^2}}} = {9.10^5}\left( {V/m} \right)\\{E_2} = k\frac{{\left| {{q_2}} \right|}}{{{r^2}}} = {9.10^9}\frac{{\left| {{{3.6.10}^{ - 6}}} \right|}}{{{{0,1}^2}}} = {194,4.10^5}\left( {V/m} \right)\end{array}\) Cường độ điện trường tổng hợp gây ra tại M là: \(\overrightarrow E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} = > \overrightarrow {{E_1}} \uparrow \uparrow \overrightarrow {{E_2}} = > E = {E_1} + {E_2} = {203,4.10^5}\left( {V/m} \right)\) Câu hỏi 49 : Một điện tích điểm \({q_1} = + {9.10^{ - 6}}C\) đặt tại điểm O trong chân không. Xét điểm M nằm cách \({q_1}\) một khoảng 20cm. a) Tính độ lớn của cường độ điện trường do điện tích điểm \({q_1}\) gây ra tại điểm M. b) Người ta đặt tại M một điện tích điểm \({q_2} = + 4\mu C\). Tính độ lớn của lực điện trường tác dụng lên điên tích \({q_2}\). Phương pháp giải: a) Vận dụng biểu thức: \(E = k\dfrac{{\left| Q \right|}}{{{r^2}}}\) b) Sử dụng biểu thức định luật Cu-lông: \(F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\) hoặc \(F = qE\) Lời giải chi tiết: a) Cường độ điện trường do điện tích \({q_1}\) gây ra tại M: \(E = k\dfrac{{\left| {{q_1}} \right|}}{{{r^2}}} = {9.10^9}\dfrac{{\left| {{{9.10}^{ - 6}}} \right|}}{{0,{2^2}}} = 20,{25.10^5}V/m\) b) Lực điện trường tác dụng lên \({q_2}\) là: \(F = {q_2}E = {4.10^{ - 6}}.20,{25.10^5} = 8,1N\) Câu hỏi 50 : Cho hai điện tích điểm \({q_1} = {6.10^{ - 7}}C\) và \({q_2} = - {8.10^{ - 7}}C\) đặt tại hai điểm A và B trong không khí cách nhau \(5cm\). a. Xác định véc tơ cường độ điện trường tổng hợp tại M do \({q_1}\) và \({q_2}\) gây ra biết \(MA = 3cm,\) \(MB = 8cm\). b. Đặt điện tích \({q_3}\) tại điểm M sao cho lực điện tổng hợp do \({q_2}\) và \({q_3}\) tác dụng lên \({q_1}\) bằng 0. Xác định dấu và độ lớn của \({q_3}\). Phương pháp giải: a. Vận dụng biểu thức tính lực điện: \(F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\) và tổng véc tơ cường độ điện trường. b. Vận dụng điều kiện cân bằng của điện tích. Lời giải chi tiết:
+ Cường độ điện trường do điện tích \({q_1}\) gây ra tại M: \({E_1} = k\dfrac{{\left| {{q_1}} \right|}}{{A{M^2}}} = {9.10^9}\dfrac{{\left| {{{6.10}^{ - 7}}} \right|}}{{0,{{03}^2}}} = {60.10^5}V/m\) + Cường độ điện trường do điện tích \({q_2}\) gây ra tại M: \({E_2} = k\dfrac{{\left| {{q_2}} \right|}}{{B{M^2}}} = {9.10^9}\dfrac{{\left| { - {{8.10}^{ - 7}}} \right|}}{{0,{{08}^2}}} = 11,{25.10^5}V/m\) Cường độ điện trường tổng hợp tại M: \(\overrightarrow E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} \) Ta có \(\overrightarrow {{E_1}} \uparrow \downarrow \overrightarrow {{E_2}} \) \( \Rightarrow E = \left| {{E_1} - {E_2}} \right| = {60.10^5} - 11,{25.10^5} = 48,{75.10^5}V/m\) b. Lực điện do \({q_2}\) tác dụng lên \({q_1}\): \({F_{21}} = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{A{B^2}}}\) Lực điện do \({q_3}\) tác dụng lên \({q_1}\): \({F_{31}} = k\dfrac{{\left| {{q_1}{q_3}} \right|}}{{A{M^2}}}\) Ta có hợp lực tác dụng lên \({q_1}\): \(\overrightarrow {{F_{21}}} + \overrightarrow {{F_{31}}} = \overrightarrow 0 \) \( \Rightarrow \overrightarrow {{F_{21}}} = - \overrightarrow {{F_{31}}} \) \( \Rightarrow \) \(\left\{ \begin{array}{l}\overrightarrow {{F_{31}}} \uparrow \downarrow \overrightarrow {{F_{21}}} \\{F_{31}} = {F_{21}}\end{array} \right.\) \( \Rightarrow {q_3} < 0\)
\(\begin{array}{l}{F_{31}} = {F_{21}} \Leftrightarrow k\dfrac{{\left| {{q_1}{q_3}} \right|}}{{A{M^2}}} = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{A{B^2}}}\\ \Leftrightarrow \dfrac{{\left| {{q_3}} \right|}}{{A{M^2}}} = \dfrac{{\left| {{q_2}} \right|}}{{A{B^2}}}\\ \Rightarrow \left| {{q_3}} \right| = \dfrac{{\left| {{q_2}} \right|}}{{A{B^2}}}A{M^2} = \dfrac{{\left| { - {{8.10}^{ - 7}}} \right|}}{{0,{{05}^2}}}.0,{03^2} = 2,{88.10^{ - 7}}\\ \Rightarrow {q_3} = - 2,{88.10^{ - 7}}C\end{array}\) Quảng cáo
|