Câu hỏi:
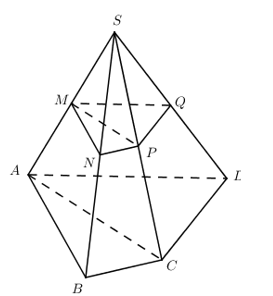
Cho hình chóp S.ABCD, M là trung điểm của SA. Gọi \(\left( \alpha \right)\) là mặt phẳng qua M và song song với mặt phẳng (ABCD). Mặt phẳng \(\left( \alpha \right)\) chia khối chóp S.ABCD thành hai khối gồm khối chứa điểm S có thể tích \({V_1}\) và khối chứa điểm A có thể tích V2. Tính tỉ số \(\frac{{{V_1}}}{{{V_2}}}\)?
- A \(\frac{{{V_1}}}{{{V_2}}} = 1\)
- B \(\frac{{{V_1}}}{{{V_2}}} = \frac{1}{7}\)
- C \(\frac{{{V_1}}}{{{V_2}}} = \frac{1}{2}\)
- D \(\frac{{{V_1}}}{{{V_2}}} = \frac{1}{8}\)
Phương pháp giải:
Sử dụng công thức tỉ số thể tích.
Lời giải chi tiết:
Gọi N, P, Q lần lượt là trung điểm của SB, SC, SD ta có \(\left( {MNPQ} \right)//\left( {ABCD} \right) \Rightarrow \left( {MNPQ} \right) \equiv \left( \alpha \right)\)
Ta có:
\(\begin{array}{l}\frac{{{V_{SMNP}}}}{{{V_{S.ABC}}}} = \frac{{SM}}{{SA}}.\frac{{SN}}{{SB}}.\frac{{SP}}{{SC}} = \frac{1}{2}.\frac{1}{2}.\frac{1}{2} = \frac{1}{8} \Rightarrow {V_{SMNP}} = \frac{1}{8}{V_{S.ABC}}\\\frac{{{V_{SMPQ}}}}{{{V_{S.ACD}}}} = \frac{{SM}}{{SA}}.\frac{{SP}}{{SC}}.\frac{{SQ}}{{SD}} = \frac{1}{2}.\frac{1}{2}.\frac{1}{2} = \frac{1}{8} \Rightarrow {V_{SMPQ}} = \frac{1}{8}{V_{S.ACD}}\\ \Rightarrow {V_1} = {V_{SMNP}} + {V_{SMPQ}} = \frac{1}{8}\left( {{V_{S.ABC}} + {V_{S.ACD}}} \right) = \frac{1}{8}{V_{S.ABCD}}\\ \Rightarrow \frac{{{V_1}}}{{{V_2}}} = \frac{1}{7}\end{array}\)
Chọn B.