Câu hỏi:
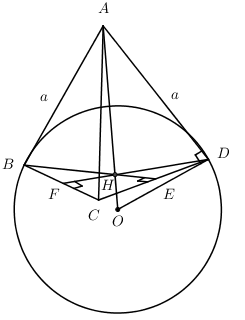
Tứ diện đều ABCD có AB = a. Mặt cầu (S) tiếp xúc với AB, AC, AD tại B, C, D. Tính thể tích cầu (S).
- A \(\pi {{a}^{3}}\)
- B \(\frac{\pi {{a}^{3}}}{3\sqrt{2}}\)
- C \(\frac{\pi {{a}^{3}}}{3}\)
- D \(\frac{2\pi {{a}^{3}}}{3\sqrt{2}}\)
Phương pháp giải:
Lời giải chi tiết:
+) Vẽ H là tâm tam giác BCD \(\Rightarrow AH\bot \left( BCD \right)\)
+) Gọi O là tâm cầu ta có thể nhận xét \(O\in AH\) và \(\widehat{ADO}={{90}^{o}}\)
+) \(DH=\frac{2}{3}DF=\frac{2}{3}.\frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{3}\)
+) Trong tam giác vuông ADO có:
\(\frac{1}{D{{H}^{2}}}=\frac{1}{D{{A}^{2}}}+\frac{1}{O{{D}^{2}}}\Rightarrow \frac{1}{O{{D}^{2}}}=\frac{9}{3{{a}^{2}}}-\frac{1}{{{a}^{2}}}=\frac{2}{{{a}^{2}}}\Rightarrow OD=\frac{a}{\sqrt{2}}\)
+) Thể tích khối cầu (S) là: \({{V}_{\left( S \right)}}=\frac{4}{3}\pi {{R}^{3}}=\frac{4}{3}\pi .\frac{{{a}^{3}}}{2\sqrt{2}}=\frac{2\pi {{a}^{3}}}{3\sqrt{2}}\)
Chọn đáp án D