Câu hỏi:
Cho hai điểm A, B cố định. Số \(k>0;\,0<AB<k\sqrt{2}\)
a) Tìm quỹ tích M để \(M{{A}^{2}}+M{{B}^{2}}={{k}^{2}}\) không đổi
b) Tìm quỹ tích M để \(M{{A}^{2}}+2M{{B}^{2}}+3M{{C}^{2}}={{k}^{2}}\)
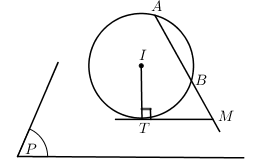
c) Cho A, B cùng phía mặt phẳng (P) và không song song với mặt phẳng (P). Xét các mặt cầu qua A, B tiếp xúc với (P) tại T. Tìm quỹ tích T
Phương pháp giải:
Lời giải chi tiết:
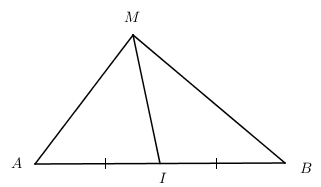
a) +) Vẽ I là trung điểm của AB. Ta có:
\(M{{A}^{2}}+M{{B}^{2}}=2M{{I}^{2}}+\frac{A{{B}^{2}}}{2}={{k}^{2}}\Rightarrow MI=\frac{1}{2}.\sqrt{2{{k}^{2}}-A{{B}^{2}}}\) không đổi
Þ Qũy tích M là mặt cầu (S) tâm I, bán kính \(R=\frac{1}{2}\sqrt{2{{k}^{2}}-A{{B}^{2}}}\)
b) Xét 3 điểm A, B, C tạo ra một tam giác (HS tự giải)
c) +) \(AB\cap (P)=M.\) Ta có:
\(M{{T}^{2}}=MA.MB\Rightarrow MT=\sqrt{MA.MB}\)
Þ Qũy tích điểm T là đường tròn (C) có tâm M, bán kính \(R=\sqrt{MA.MB}\)
Câu hỏi trước
