Phương pháp giải:

Lời giải chi tiết:

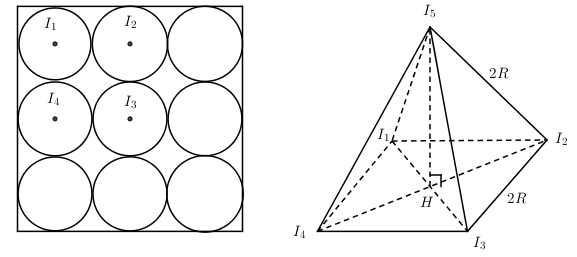
+) Vì cạnh đáy hộp bằng 6R. Đường kính mỗi quả cầu là 2R nên ta có thể xếp được 9 quả cầu tiếp xúc nhau vào đáy hộp để các cầu tiếp xúc thành hộp

+) Xét 4 cầu (S₁), (S₂), (S₃), (S₄) có tâm lần lượt là I₁, I₂, I₃, I₄. Ta đặt cầu (S₅) lên chỗ lóm 4 cầu trên.

+) Chóp I₅I₁I₂I₃I₄  là chóp đều có tất cả các cạnh bằng 2R.

+) \(H{{I}_{2}}=R\sqrt{2}\)

+) Trong \({{\Delta }_{v}}{{I}_{5}}H{{I}_{2}}\) có: \({{I}_{5}}H=\sqrt{{{I}_{5}}{{I}_{2}}^{2}-{{I}_{2}}{{H}^{2}}}=\sqrt{4{{R}^{2}}-2{{R}^{2}}}=\sqrt{2}R\)

+) Chiều cao cả hệ là:\(h=\sqrt{2}R+2R\approx 3,14R<3,5R\)

+) Vậy có thể đặt 4 cầu vào 4 chỗ lõm và tổng số cầu được đặt vào hình hộp tối đa là 13

Chọn đáp án B