Câu hỏi:
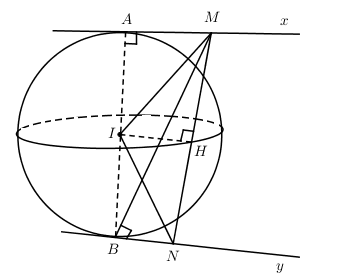
Cho mặt cầu (S) có đường kính AB = 10. Vẽ các tiếp tuyến Ax, By với mặt cầu (S) sao cho \(Ax\bot By.\) M di động trên Ax, N di động trên By sao cho MN luôn tiếp xúc với mặt cầu. Tính \(P=AM.BN\)
- A 40
- B 50
- C 100
- D 120
Phương pháp giải:
Lời giải chi tiết:
* Giả sử MN tiếp xúc (S) tại H \(\Rightarrow IH\bot MN\)
* \(\left\{ \begin{align} & BN\bot AB \\ & BN\bot AM \\ \end{align} \right.\Rightarrow BN\bot \left( ABM \right)\Rightarrow BN\bot BM\)
* \(\Delta\) vuông BMN có: \(M{{N}^{2}}=B{{M}^{2}}+B{{N}^{2}}\)
\(\begin{array}{l}
\Rightarrow {\left( {HM + HN} \right)^2} = B{M^2} + B{N^2}\\
\Rightarrow {\left( {AM + BN} \right)^2} = \left( {A{B^2} + A{M^2}} \right) + B{N^2}\\
\,\left( {Do:\left\{ \begin{array}{l}
HM = AM\\
NH = NB
\end{array} \right.} \right)\\
\Rightarrow A{B^2} = 2AM.BN \Rightarrow AM.BN = \frac{{A{B^2}}}{2} = 50
\end{array}\)
Chọn đáp án B