Phương pháp giải:

Lời giải chi tiết:

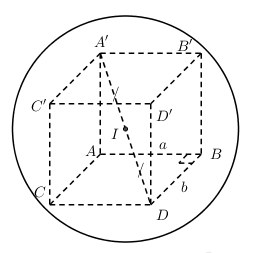
* Đặt AB = a, BC = b, AA’ = c (a, b, c > 0)

* Diện tích toàn phần hình hộp chữ nhật nội tiếp cầu: ${{S}_{tp}}=2\left( ab+bc+ca \right)$

* Bất đẳng thức Cosi: $\left\{ \begin{align}  & {{a}^{2}}+{{b}^{2}}\ge 2ab \\ & {{b}^{2}}+{{c}^{2}}\ge 2bc \\ & {{c}^{2}}+{{a}^{2}}\ge 2ca \\ \end{align} \right.\Rightarrow 2\left( {{a}^{2}}+{{b}^{2}}+{{c}^{2}} \right)\ge {{S}_{tp}}$

$\Rightarrow {{S}_{tp}}\le 2\left( {{a}^{2}}+{{b}^{2}}+{{c}^{2}} \right)=2A'{{C}^{2}}=8{{R}^{2}}$

$\Rightarrow$ S_tp lớn nhất bẳng $8{{R}^{2}}\Leftrightarrow a=b=c=\frac{2R}{\sqrt{3}}$

Khi đó hình hộp có diện tích toàn phần lớn nhất có thể tích là: $V={{a}^{3}}={{\left( \frac{2R}{\sqrt{3}} \right)}^{3}}=\frac{8{{R}^{3}}}{3\sqrt{3}}$

Chọn đáp án A