Câu hỏi:
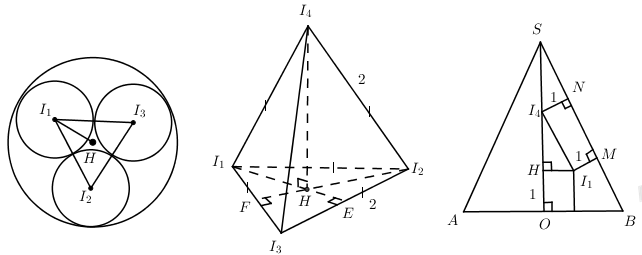
Người ta xếp 4 quả cầu có R = 1 vào trong hình nón, để 3 quả cầu tiếp xúc đáy nón, tiếp xúc nhau và tiếp xúc với mặt xung quanh nón. Quả thứ 4 tiếp xúc 3 quả trên và tiếp xúc mặt xung quanh nón. Tính chiều cao của hình nón.
- A \(\frac{3\sqrt{3}+3+2\sqrt{6}}{3}\)
- B \(\frac{3+\sqrt{3}+\sqrt{6}}{3}\)
- C \(\frac{3+\sqrt{3}+\sqrt{2}}{3}\)
- D \(\frac{3\sqrt{3}+3+\sqrt{6}}{3}\)
Phương pháp giải:
Lời giải chi tiết:
+) Tam giác đều \({{I}_{1}}{{I}_{2}}{{I}_{3}}:\,{{I}_{1}}H=\frac{2}{3}.2.\frac{\sqrt{3}}{2}=\frac{2\sqrt{3}}{3}\)
+) \({{\Delta }_{v}}{{I}_{4}}H{{I}_{1}}:\,{{I}_{4}}H=\sqrt{4-\frac{12}{9}}=\frac{\sqrt{24}}{3}=\frac{2\sqrt{6}}{3}\)
+) Ta có: \({{I}_{1}}{{I}_{4}}\parallel MN\Rightarrow \widehat{NS{{I}_{4}}}=\widehat{{{I}_{1}}{{I}_{4}}H}\)
\(+)\Rightarrow {{\Delta }_{v}}SN{{I}_{4}}\sim {{\Delta }_{v}}{{I}_{4}}H{{I}_{1}}\Rightarrow \frac{S{{I}_{4}}}{{{I}_{1}}{{I}_{4}}}=\frac{{{I}_{4}}N}{{{I}_{1}}H}\Rightarrow S{{I}_{4}}=\frac{2.1}{\frac{2\sqrt{3}}{3}}=\sqrt{3}\)
+) Chiều cao của hình nón là: \(h=S{{I}_{4}}+{{I}_{4}}H+1=1+\sqrt{3}+\frac{2\sqrt{6}}{3}=\frac{3+3\sqrt{3}+2\sqrt{6}}{3}\)
Chọn đáp án A