Câu hỏi:
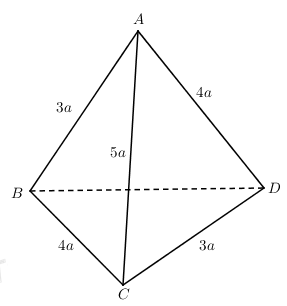
Tứ diện \(ABCD\) có: \(AB = CD = 3a\), \(BC = AD = 4a\), \(AC = 5a\). Tính thể tích khối cầu ngoại tiếp tứ diện \(ABCD\).
- A \(\dfrac{115\pi {{a}^{3}}}{8}\)
- B \(\dfrac{125\pi {{a}^{3}}}{6}\)
- C \(\dfrac{100\pi {{a}^{3}}}{3}\)
- D \(\dfrac{175\pi {{a}^{3}}}{8}\)
Phương pháp giải:
Lời giải chi tiết:
+) Nhận xét: \(\Delta ADC\) vuông tại \(D\) và \(\Delta ABC\) vuông tại \(B\).
+) \(R=\dfrac{AC}{2}=\dfrac{5a}{2}\)
+) Vcầu\(=\dfrac{4}{3}\pi {{R}^{3}}=\dfrac{4}{3}\pi .{{\left( \dfrac{5a}{2} \right)}^{3}}=\dfrac{4\pi }{3}.\dfrac{125{{a}^{3}}}{8}=\dfrac{125\pi {{a}^{3}}}{6}\)
Chọn đáp án B.
Quảng cáo
Câu hỏi trước
