Câu hỏi:
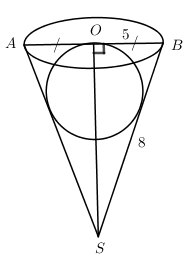
Có một cái cốc hình nón đường kính đáy bằng \(10\), đường sinh bằng \(8\). Người ta thả một viên bi hình cầu vào cốc sao cho không phần nào của viên bi cao hơn miệng cốc. Hỏi bán kính \(R\) lớn nhất của viên bi là bao nhiêu?
- A \(\dfrac{5\sqrt{39}}{13}\)
- B \(\dfrac{\sqrt{39}}{13}\)
- C \(\dfrac{5}{13}\)
- D \(\dfrac{3\sqrt{39}}{13}\)
Phương pháp giải:
Lời giải chi tiết:
* Nhận xét: Viên bi lớn nhất có bán kính \(R\) bằng bán kính đường tròn nội tiếp tam giác \(SAB\).
\(\begin{align} & SO=\sqrt{S{{B}^{2}}-O{{B}^{2}}}=\sqrt{{{8}^{2}}-{{5}^{2}}}=\sqrt{39} \\ & R=\frac{{{S}_{\Delta SAB}}}{P}=\dfrac{\dfrac{1}{2}.10.\sqrt{39}}{13}=\dfrac{5\sqrt{39}}{13} \\ \end{align}\)
Chọn đáp án A.
Quảng cáo
Câu hỏi trước
