Câu hỏi:
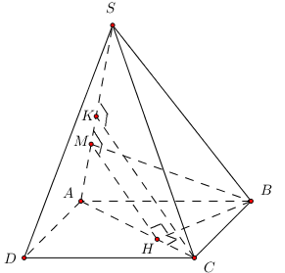
Chóp S.ABCD, ABCD là hình chữ nhật. AB = 3; BC = 4, \(\left( {SAC} \right) \bot \left( {ABCD} \right);\,\,d\left( {C;SA} \right) = 4\). Tisnh \(\cos \left( {\left( {SAB} \right);\left( {SAC} \right)} \right)\)?
- A \(\frac{3}{{\sqrt {31} }}\)
- B \(\frac{3}{{\sqrt {33} }}\)
- C \(\frac{3}{{\sqrt {34} }}\)
- D \(\frac{3}{{\sqrt {35} }}\)
Phương pháp giải:
Lời giải chi tiết:
* Vẽ \(CK \bot SA \Rightarrow CK = 4\)
* Vẽ \(BH \bot AC \Rightarrow BH \bot \left( {SAC} \right)\)
Vẽ \(HM \bot SA \Rightarrow \widehat {\left( {\left( {SAB} \right);\left( {SAC} \right)} \right)} = \widehat {BMH}\)
* Xét tam giác vuông ABC: \(\frac{1}{{B{H^2}}} = \frac{1}{9} + \frac{1}{{16}} \Rightarrow BH = \frac{{12}}{5}\)
Và \(\frac{{AH}}{{AC}} = \frac{{A{B^2}}}{{A{C^2}}} = \frac{9}{{25}}\)
* HM // CK \( \Rightarrow \frac{{MH}}{{CK}} = \frac{{AH}}{{AC}} = \frac{9}{{25}} \Rightarrow MH = \frac{9}{{25}}.4 = \frac{{36}}{{25}}\)
* Xét tam giác vuông MHB:
\(MB = \sqrt {M{H^2} + H{B^2}} = \sqrt {\frac{{{{36}^2}}}{{{{25}^2}}} + \frac{{{{12}^2}}}{{{5^2}}}} = \frac{{2\sqrt {34} }}{{25}}\)
* Xét tam giác vuông BHM: \(\cos \widehat M = \frac{{MH}}{{MB}} = \frac{{36}}{{25}}:\frac{{12\sqrt {34} }}{{25}} = \frac{3}{{\sqrt {34} }}\)
Chọn đáp án C.