Phương pháp giải:

Lời giải chi tiết:

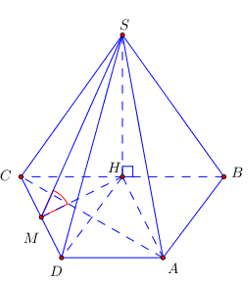
* Vẽ \(SH \bot BC \Rightarrow H\) là trung điểm BC và \(SH = 2a.\frac{{\sqrt 3 }}{2} = a\sqrt 3 \)

* Tứ giác ADCH là hình thoi

\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}AC \bot DH\\AC \bot SD\end{array} \right. \Rightarrow AC \bot \left( {SHD} \right)\\ \Rightarrow \left\{ \begin{array}{l}AC \bot SH\\SH \bot BC\end{array} \right. \Rightarrow SH \bot \left( {ABCD} \right)\end{array}\)

* Vẽ \(HM \bot CD \Rightarrow \widehat {\left( {\left( {SCD} \right);\left( {ABCD} \right)} \right)} = \widehat {SMH} = \widehat {{M_1}}\)

* \(\Delta HCD\) đêu \( \Rightarrow HM = \frac{{a\sqrt 3 }}{2}\)

* \(\Delta SHM\) vuông \( \Rightarrow \tan \widehat {{M_1}} = \frac{{SH}}{{HM}} = a\sqrt 3 :\frac{{a\sqrt 3 }}{2} = 2\)

Chọn đáp án A.