Câu hỏi:
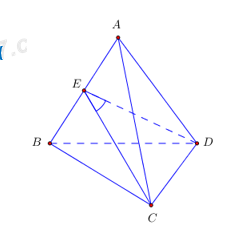
Cho tứ diện đều ABCD. Cosin của góc giữa hai mặt phẳng (ABC) và (ABD) bằng:
- A
\(\frac{1}{4}\)
- B
\(\frac{1}{3}\)
- C
\(\frac{2}{3}\)
- D \(\frac{1}{5}\)
Phương pháp giải:
Sử dụng phương pháp xác định góc giữa hai mặt phẳng và áp dụng định lí Cosin trong tam giác.
Lời giải chi tiết:
Gọi E là trung điểm của AB ta có
\(BE \bot AB;\,\,CE \bot AB \Rightarrow \widehat {\left( {\left( {ABC} \right);\left( {ABD} \right)} \right)} = \widehat {\left( {CE;DE} \right)}\)
Ta có \(CE = DE = \frac{{a\sqrt 3 }}{2};\,\,CD = a\)
Áp dụng định lí Cosin trong tam giác ECD :
\(\cos \widehat {CED} = \frac{{C{E^2} + D{E^2} - C{D^2}}}{{2.CE.DE}} = \frac{1}{3}\)
Chọn B.