Câu hỏi:
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi cạnh bằng \(a,\,\,\,\widehat{BAC}={{60}^{0}},\) cạnh \(SC\) vuông góc với đáy và \(SC=\frac{a\sqrt{6}}{2}.\) Tang của góc giữa hai mặt phẳng \(\left( SBD \right)\) và \(\left( SAD \right)\) bằng
- A
\(\frac{\sqrt{14}}{7}.\)
- B
\(\frac{\sqrt{35}}{7}.\)
- C
\(\frac{\sqrt{5}}{2}.\)
- D \(\frac{\sqrt{10}}{5}.\)
Phương pháp giải:
Sử dụng phương pháp xác định góc giữa hai mặt phẳng trong không gian
Lời giải chi tiết:
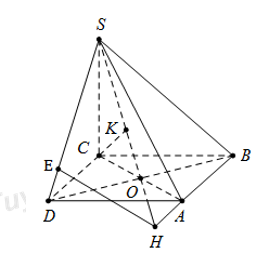
Gọi \(O\) là tâm của hình thoi \(ABCD,\) kẻ \(\left\{ \begin{align} CK\bot SO\,\,\,\left( K\in SO \right) \\ AH\bot SO\,\,\,\left( H\in SO \right) \\ \end{align} \right.\)
Ta dễ dàng tính được BD = a, \(\text{AC=a}\sqrt{3}\)
Xét tam giác vuông SCO có :
\(CK=\frac{SC.CO}{\sqrt{S{{C}^{2}}+C{{O}^{2}}}}=\frac{\frac{a\sqrt{6}}{2}.\frac{a\sqrt{3}}{2}}{\sqrt{{{\left( \frac{a\sqrt{6}}{2} \right)}^{2}}+{{\left( \frac{a\sqrt{3}}{2} \right)}^{2}}}}=\frac{a}{\sqrt{2}}\)
\(\begin{align} \Rightarrow AH=CK=\frac{a}{\sqrt{2}};\,\,SO=\sqrt{S{{C}^{2}}+O{{C}^{2}}}=\frac{3a}{2} \\ OK=\frac{C{{O}^{2}}}{SO}=\frac{\frac{3{{a}^{2}}}{4}}{\frac{3a}{2}}=\frac{a}{2} \\ \Rightarrow SH=SO+OH=SO+OK=\frac{3a}{2}+\frac{a}{2}=2a. \\ \end{align}\)
Ta có : \(\left\{ \begin{align} BD\bot SC \\ BD\bot AC \\ \end{align} \right.\Rightarrow BD\bot \left( SAC \right)\Rightarrow BD\bot AH\)
\(\left\{ \begin{align} AH\bot BD \\ AH\bot SO \\ \end{align} \right.\Rightarrow AH\bot \left( SBD \right)\Rightarrow AH\bot SD\)
Kẻ \(HE\)\(\bot \)\(SD\) ta có : \(\left\{ \begin{align} SD\bot AH \\ SD\bot HE \\\end{align} \right.\Rightarrow SD\bot \left( AHE \right)\Rightarrow SD\bot AE\) \(\Rightarrow\widehat{\left( SBD \right);\left( SAD \right)}=\widehat{\left( HE;AE \right)}=\widehat{HEA}.\)
Lại có \(SD=\sqrt{S{{C}^{2}}+C{{D}^{2}}}=\frac{a\sqrt{10}}{2}\Rightarrow HE.SD=DO.SH\Rightarrow HE=\frac{2a}{\sqrt{10}}.\)
Do đó, giá trị \(\tan \widehat{HEA}=\frac{AH}{HE}=\frac{\sqrt{5}}{2}.\)
Chọn C.


















