Câu hỏi:
Cho khối lăng trụ đứng \(ABC.\,{A}'{B}'{C}'\) có đáy \(ABC\) là tam giác vuông cân tại \(A\) với \(AB=a,\,\,{A}'B\) tạo với mặt phẳng \(\left( ABC \right)\) một góc \(\alpha .\) Biết \(A{A}'.{{S}_{\Delta \,ABC}}=\frac{{{a}^{3}}\sqrt{3}}{2}.\) Tính \(\alpha .\)
- A
\(\alpha ={{70}^{0}}.\)
- B
\(\alpha ={{30}^{0}}.\)
- C
\(\alpha ={{45}^{0}}.\)
- D \(\alpha ={{60}^{0}}.\)
Phương pháp giải:
Áp dụng phương pháp xác định góc giữa đường thẳng và mặt phẳng
Lời giải chi tiết:
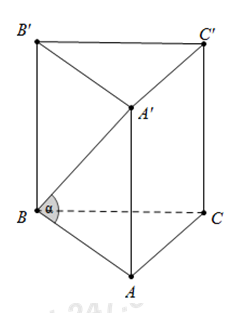
Diện tích tam giác \(ABC\) là \({{S}_{\Delta \,ABC}}=\frac{A{{B}^{2}}}{2}=\frac{{{a}^{2}}}{2}\Rightarrow A{A}'=a\sqrt{3}.\)
Do \(A{A}'\bot \left( ABC \right)\Rightarrow \widehat{{A}'BA}=\alpha \Rightarrow \tan \alpha =\frac{A{A}'}{AB}=\sqrt{3}\Rightarrow \alpha ={{60}^{0}}.\)
Chọn D
Quảng cáo
Câu hỏi trước
