Câu hỏi:
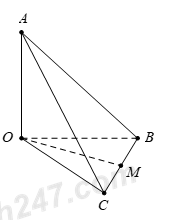
Cho tứ diện \(OABC\) có \(OA,\,\,OB,\,\,OC\) đôi một vuông góc với nhau và \(OA=OB=OC.\) Gọi \(M\) là trung điểm của \(BC\) (tham khảo hình vẽ bên). Góc giữa hai đường thẳng \(OM\) và \(AB\) bằng
- A
\({{90}^{0}}.\)
- B
\({{30}^{0}}.\)
- C
\({{60}^{0}}.\)
- D \({{45}^{0}}.\)
Phương pháp giải:
Áp dụng phương pháp xác định góc giữa hai đường thẳng bằng cách dựng hình hoặc tính tích vô hướng của hai vectơ trong không gian
Lời giải chi tiết:
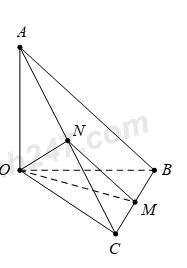
Gọi \(N\) là trung điểm của \(AC\)x\(\Rightarrow MN\) // AB (đường trung bình tam giác).
Suy ra \(\widehat{\left( OM;AB \right)}=\widehat{\left( OM;MN \right)}=\widehat{OMN}=\alpha \) với \({{0}^{0}}<\alpha <{{90}^{0}}.\)
Tam giác \(OMN\) có \(OM=ON=\frac{a\sqrt{2}}{2};\,\,MN=\frac{a\sqrt{2}}{2}\)\(\Rightarrow \)\(\Delta \,OMN\) đều.
Do đó \(\widehat{OMN}={{60}^{0}}.\) Vậy góc giữa hai đường thẳng \(OM,\,\,AB\) là \({{60}^{0}}.\)
Chọn C
Câu hỏi trước
