Câu hỏi:
Cho tứ diện \(ABCD\) có\(AB=4a\), \(CD=6a\), các cạnh còn lại có độ dài bằng\(a\sqrt{22}\). Tính bán kính \(R\) của mặt cầu ngoại tiếp tứ diện\(ABCD\).
- A \(R=\frac{a\sqrt{79}}{3}\).
- B \(R=\frac{5a}{2}\).
- C \(R=\frac{a\sqrt{85}}{3}\).
- D \(R=3a\).
Phương pháp giải:
+) Xác định chiều cao hạ từ đỉnh \(A\) của tứ diện, từ các giả thiết suy ra tâm mặt cầu nằm trên đoạn \(MN\).
+) Xác định tâm đường tròn ngoại tiếp đáy \(BCD\).
+) Từ tâm kẻ đường thẳng song song với đường cao hạ từ \(A\), đường thẳng này cắt \(MN\) tại \(O\) là tâm mặt cầu cần tìm.
+) Dựa vào định lý Pytago để tính bán kính.
Lời giải chi tiết:
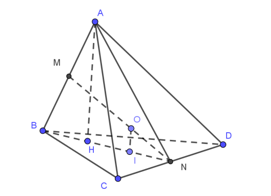
Gọi \(M,\)\(N,\) lần lượt là trung điểm các cạnh \(AB,\)\(CD\). Ta có \(\Delta ACD=\Delta BCD\)(c-c-c) nên \(AN=BN\)do đó tam giác \(NAB\) cân tại \(N\)\(\Rightarrow MN\bot AB\)
Tương tự ta có \(MN\bot CD\)
Ta có \(\left( ABN \right)\bot CD\)\(\Rightarrow \left( ABN \right)\bot \left( BCD \right)\)
mà \(\left( ABN \right)\cap \left( BCD \right)=BN\). Trong \(\left( ABN \right)\)kẻ \(AH\bot BN\Rightarrow AH\bot \left( BCD \right)\)
Gọi \(I\)là tâm đường tròn ngoại tiếp tam giác BCD. Dựng trục It, gọi \(O=It\cap MN\) khi đó \(O\) là tâm mặt cầu ngoại tiếp tứ diện. Gọi \(R\) là bán kính mặt cầu ngoại tiếp tứ diện.
Ta có \(M{{N}^{2}}=A{{N}^{2}}-A{{M}^{2}}\)\(=A{{D}^{2}}-N{{D}^{2}}-A{{M}^{2}}=9{{a}^{2}}\)\(\Rightarrow MN=3a.\)
Ta có \(O{{A}^{2}}=O{{D}^{2}}\Leftrightarrow O{{M}^{2}}+M{{A}^{2}}=O{{N}^{2}}+N{{D}^{2}}={{R}^{2}}\)
\(\Rightarrow O{{M}^{2}}-O{{N}^{2}}=N{{D}^{2}}-M{{A}^{2}}=9{{a}^{2}}-4{{a}^{2}}=5{{a}^{2}}\)
\(\Rightarrow \left( OM-ON \right)\left( OM+ON \right)=5{{a}^{2}}\)
Mà \(OM+ON=MN=3a\)\(\Rightarrow OM-ON=\frac{5}{3}a\)
Từ \(\left\{ \begin{array}{l}OM + ON = 3a\\OM - ON = \frac{5}{3}a\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}OM = \frac{7}{3}a\\ON = \frac{2}{3}a\end{array} \right.\)
Ta có \(R=\sqrt{O{{N}^{2}}+N{{D}^{2}}}=\sqrt{{{\left( \frac{2}{3}a \right)}^{2}}+{{\left( 3a \right)}^{2}}}=\frac{a\sqrt{85}}{3}\).
Chọn C.


















