Câu hỏi:
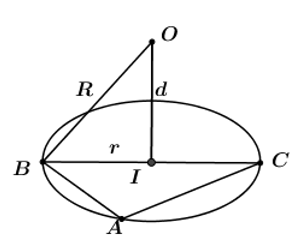
Cho mặt cầu (S) tâm O và các điểm A, B, C nằm trên mặt cầu (S) sao cho \(AB=3;\ \ AC=4;\) \(BC=5\) và khoảng cách từ O đến mặt phẳng (ABC) bằng 1. Thể tích của khối cầu (S) bằng
- A \(\frac{7\sqrt{21}\pi }{2}\)
- B \(\frac{13\sqrt{13}\pi }{6}\)
- C \(\frac{20\sqrt{5}\pi }{3}\)
- D \(\frac{29\sqrt{29}\pi }{6}\)
Phương pháp giải:
+) Tính bán kính của mặt cầu dựa vào định lý Pi-ta-go: \(R=\sqrt{{{r}^{2}}+{{d}^{2}}}.\) . +) Thể tích của mặt cầu: \({{V}_{\left( S \right)}}=\frac{4}{3}\pi {{R}^{3}}.\)
Lời giải chi tiết:
Theo đề bài ta có:
\(B{{C}^{2}}=A{{C}^{2}}+A{{B}^{2}}=25\Rightarrow \Delta ABC\) là tam giác vuông tại \(A\Rightarrow \left( ABC \right)\) cắt mặt cầu theo giao tuyến là 1 đường tròn đường kính BC
\(\Rightarrow r=BI=5:2=2,5.\)
Gọi \(\left( \alpha \right)\) là mặt phẳng chứa ba điểm \(A;\ B;\ C\Rightarrow d\left( O;\left( \alpha \right) \right)=OI=1.\) \(\Rightarrow \) Bán kính mặt cầu là: \(R=\sqrt{O{{I}^{2}}+B{{I}^{2}}}=\sqrt{1+2,{{5}^{2}}}=\frac{\sqrt{29}}{2}.\)
\(\Rightarrow {{V}_{\left( S \right)}}=\frac{4}{3}\pi {{R}^{3}}=\frac{4}{3}\pi .{{\left( \frac{\sqrt{29}}{2} \right)}^{3}}=\frac{4}{3}\pi .\frac{29\sqrt{29}}{8}=\frac{29\sqrt{29}\pi }{6}.\)
Chọn D.