Phương pháp giải:

Sử dụng phương pháp xác định góc giữa hai mặt phẳng và áp dụng các hệ thức lượng trong tam giác vuông

Lời giải chi tiết:

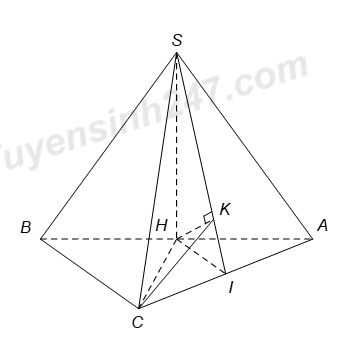
Ta có \(SH\bot \left( ABC \right)\Rightarrow SH\bot CH\).                    (1)

Tam giác ABC cân tại C nên \(CH\bot AB\).          (2)

Từ (1) và (2), suy ra \(CH\bot \left( SAB \right)\).

Gọi I là trung điểm \(AC\)\(\Rightarrow \,\,HI//BC\xrightarrow{BC\,\bot \,\,AC}HI\bot AC\). (3)

Mặt khác \(AC\bot SH\) (do \(SH\bot \left( ABC \right)\)).         (4)

Từ (3) và (4), suy ra \(AC\bot \left( SHI \right)\).

Kẻ \(HK\bot SI\text{ }\,\left( K\in SI \right)\).   (5)

Từ \(AC\bot \left( SHI \right)\Rightarrow AC\bot HK\).   (6).

Từ (5) và (6), suy ra \(HK\bot \left( SAC \right)\).

Vì \(\left\{ \begin{array}{l}HK \bot \left( {SAC} \right)\\HC \bot \left( {SAB} \right)\end{array} \right.\) nên góc giữa hai mặt phẳng \(\left( SAC \right)\) và \(\left( SAB \right)\) bằng góc giữa hai đường thẳng \(HK\) và \(HC\).

Ta có \(HK\bot \left( SAC \right)\Rightarrow HK\bot CK\Rightarrow \Delta CHK\( vuông tại K.

Có \(CH=\frac{1}{2}AB=\frac{a}{2}\); \(\frac{1}{H{{K}^{2}}}=\frac{1}{S{{H}^{2}}}+\frac{1}{H{{I}^{2}}}=\frac{1}{{{a}^{2}}}+\frac{1}{{{\left( \frac{1}{2}.\frac{a}{\sqrt{2}} \right)}^{2}}}\Rightarrow HK=\frac{a}{3}\).

Do đó \(\cos \widehat{CHK}=\frac{HK}{CH}=\frac{\frac{a}{3}}{\frac{a}{2}}=\frac{2}{3}.\)

Chọn D.