Câu hỏi:
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi cạnh \(a\), các cạnh \(SA=SB=a,\) \(SD=a\sqrt{2}\). Góc giữa hai mặt phẳng \(\left( SBD \right)\) và \(\left( ABCD \right)\) bằng \({{90}^{0}}.\) Độ dài đoạn thẳng \(BD\)
- A
bằng \(2a.\)
- B
bằng \(2a\sqrt{3}.\)
- C
bằng \(a\sqrt{3}.\)
- D \(a\sqrt{2}.\)
Phương pháp giải:
Sử dụng phương pháp xác định góc giữa hai mặt phẳng và áp dụng các hệ thức lượng trong tam giác vuông
Lời giải chi tiết:
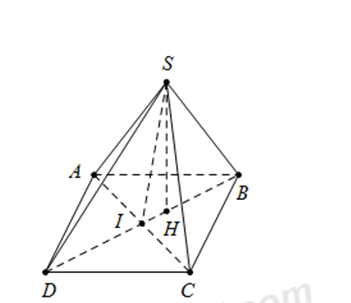
Gọi \(I\) là tâm của hình thoi \(ABCD\).
Và \(H\) là hình chiếu vuông góc của \(S\) lên \(BD\).
\(\widehat{\left( \left( SBD \right);\left( ABCD \right) \right)}={{90}^{0}}\Rightarrow \left( SBD \right)\bot \left( ABCD \right)\Rightarrow SH\bot \left( ABCD \right)\).
Khi đó \(\left\{ \begin{array}{l}SH \bot AC\\BD \bot AC\end{array} \right. \Rightarrow AC \bot \left( {SBD} \right) \Rightarrow AC \bot SI\).
\(\Delta SAC = \Delta BAC\left( {c.c.c} \right) \Rightarrow BI = SI = \frac{1}{2}BD \Rightarrow \Delta SBD\) vuông tại S.
Mà \(I\) là trung điểm của \(AC\Rightarrow \Delta SAC\) cân tại S \(\Rightarrow SA=SB=SC\).
vuông tại S
\(\Rightarrow B{{D}^{2}}=S{{B}^{2}}+S{{D}^{2}}={{a}^{2}}+{{\left( a\sqrt{2} \right)}^{2}}=3{{a}^{2}}\Rightarrow BD=a\sqrt{3}\).
Chọn C.


















