Phương pháp giải:

Sử dụng phương pháp xác định góc giữa hai mặt phẳng và áp dụng các hệ thức lượng trong tam giác vuông

Lời giải chi tiết:

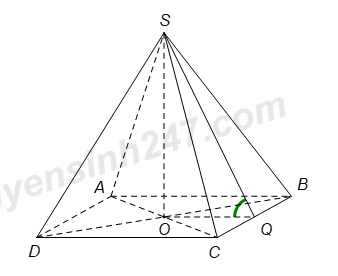
Gọi \(Q\) là trung điểm \(BC\), suy ra \(OQ\bot BC\).

Ta có \(\left\{ \begin{array}{l}BC \bot OQ\\BC \bot SO\end{array} \right. \Rightarrow BC \bot \left( {SOQ} \right) \Rightarrow BC \bot SQ.\)

Do đó

\(\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABCD} \right) = BC\\\left( {SBC} \right) \supset SQ \bot BC\\\left( {ABCD} \right) \supset OQ \bot BC\end{array} \right. \Rightarrow \widehat {\left( {\left( {SBC} \right);\left( {ABCD} \right)} \right)} = \widehat {\left( {SQ;OQ} \right)} = \widehat {SQO}.\)

Tam giác vuông \(SOQ\), có \(\tan \widehat{SQO}=\frac{SO}{OQ}=\sqrt{3}\Rightarrow \widehat{SQO}={{60}^{0}}\)

Vậy mặt phẳng \(\left( SBC \right)\) hợp với mặt đáy \(\left( ABCD \right)\) một góc \({{60}^{0}}.\)

Chọn C.