Câu hỏi:
Cho tứ diện \(S.ABC\) có \(SBC\) và \(ABC\) nằm trong hai mặt phẳng vuông góc với nhau. Tam giác \(SBC\) đều, tam giác \(ABC\) vuông tại \(A\). Gọi \(H\), \(I\) lần lượt là trung điểm của \(BC\) và \(AB\). Khẳng định nào sau đây sai?
- A
\(SH\bot AB.\)
- B
\(HI\bot AB.\)
- C
\(\left( SAB \right)\bot \left( SAC \right).\)
- D \(\left( SHI \right)\bot \left( SAB \right).\)
Phương pháp giải:
Sử dụng các định lí về hai mặt phẳng vuông góc
Lời giải chi tiết:
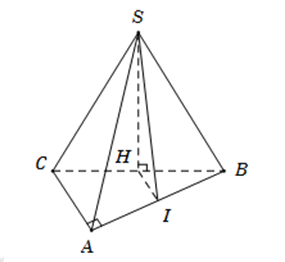
Do \(SBC\) là tam giác đều có \(H\) là trung điểm \(BC\) nên \(SH\bot BC\).
Mà \(\left( SBC \right)\bot \left( ABC \right)\) theo giao tuyến \(BC\Rightarrow SH\bot \left( ABC \right)\Rightarrow SH\bot AB.\)
\(\Rightarrow \) Đáp án A đúng.
Ta có \(HI\) là đường trung bình của \(\Delta \,ABC\) nên \(HI\parallel AC\Rightarrow HI\bot AB.\)
\(\Rightarrow \)Đáp án B đúng.
Ta có \(\left\{ \begin{array}{l}SH \bot AB\\HI \bot AB\end{array} \right. \Rightarrow AB \bot \left( {SHI} \right) \Rightarrow \left( {SAB} \right) \bot \left( {SHI} \right).\)
Đáp án D đúng.
Dùng phương pháp loại trừ thì C là đáp án sai.
Chọn C


















