Câu hỏi:
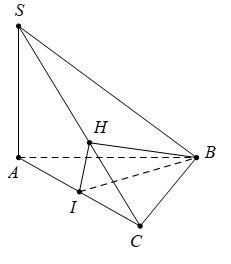
Cho tứ diện \(S.ABC\) có \(SA\) vuông góc với mặt phẳng \(\left( ABC \right)\) và tam giác \(ABC\) đều. Xác định mặt cắt của tứ diện \(S.ABC\) và mặt phẳng \(\left( \alpha \right)\) qua \(B\) và vuông góc với \(SC.\)
- A Tam giác đều.
- B Tam giác vuông.
- C Hình thang.
- D Hình thang vuông
Phương pháp giải:
Sử dụng lý thuyết của đường thẳng vuông góc với mặt phẳng và bài toán tìm giao tuyến của hai mặt phẳng
Lời giải chi tiết:
Kẻ BH vuông góc với \(SC\,\,\,\,\,\,\left( H\in SC \right).\)
Gọi I là trung điểm của AC. Ta có \(BI\bot AC\) (do \(\Delta \,ABC\) đều).
Và BI vuông góc với SA (do \(SA\bot mp\,\,\left( ABC \right)\)).
\(\Rightarrow \,\,BI\bot mp\,\,\left( SAC \right)\Rightarrow \,\,BI\bot SC.\) Từ \(\left( 1 \right),\,\,\left( 2 \right)\,\,:\,\,SC\bot mp\,\,\left( BIH \right).\)
Vậy mặt cắt là tam giác BIH vuông tại I.
Chọn B
Câu hỏi trước
