Câu hỏi:
Cho hình hộp ABCD.A’B’C’D’ có đáy ABCD là hình thoi tâm \(O,\,\,\widehat{BAD}={{60}^{0}}\) và độ dài các cạnh A’A = A’B = A’D. Hình chiếu vuông góc của A’ trên mặt phẳng (ABCD) là
- A trung điểm của OA
- B trọng tâm của tam giác ABD.
- C tâm O của hình thoi ABCD.
- D trọng tâm của tam giác BCD.
Phương pháp giải:
Sử dụng lý thuyết của đường thẳng vuông góc với mặt phẳng (điều kiện để đường thẳng vuông góc với mặt phẳng) và tính chất của đường tròn ngoại tiếp tam giác
Lời giải chi tiết:
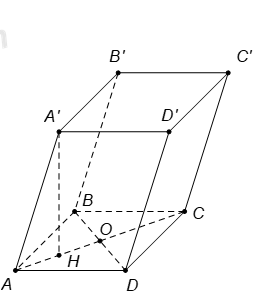
Vì ABCD là hình thoi \(\Rightarrow \)AB = AD mà \(\widehat{BAD}={{60}^{0}}\) suy ra tam giác ABD đều (1).
Ta có A’A = A’B = A’B nên hình chiếu vuông góc của A’ trên mặt phẳng (ABCD) trùng với tâm I của đường tròn ngoại tiếp tam giác ABD. (2)
Từ (1), (2) suy ra I là tâm đường tròn ngoại tiếp tam giác ABD. Mà tam giác ABD đều nên I cũng là trọng tâm của tam giác ABD.
Chọn B.


















