Phương pháp giải:

Sử dụng lý thuyết của đường thẳng vuông góc với mặt phẳng

Lời giải chi tiết:

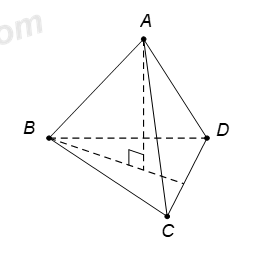Vì AH vuông góc với mp(BCD) suy ra \(AH\bot CD.\)   \(\left( 1 \right)\)

Mà H là trực tâm của tam giác BCD\(\Rightarrow \,\,BH\bot CD.\)   \(\left( 2 \right)\)

Từ \(\left( 1 \right),\left( 2 \right)\) suy ra \(\left\{ \begin{array}{l}CD \bot AH\\CD \bot BH\end{array} \right. \Rightarrow CD \bot \left( {ABH} \right) \Rightarrow CD \bot AB.\)

Chọn D.