Phương pháp giải:

Lời giải chi tiết:

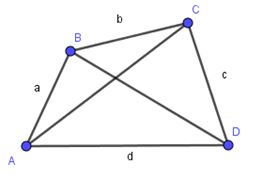
Đặt \(AB=a,BC=b,CD=c,DA=d\) .

Áp dụng kết quả câu 4 ta có: \(AC+BD>a+c\)

                                               \(AC+BD>b+d\)

Do đó: \(2\left( AC+BD \right)>a+b+c+d\)

Suy ra \(AC+BD>\frac{a+b+c+d}{2}\) .

Xét tam giác ABC có: \(AC<a+b\) .                                            

Xét tam giác ADC có: \(AC<c+d\).

Do đó: \(2AC<a+b+c+d\)

Suy ra: \(AC<\frac{a+b+c+d}{2}\)

Tương tự ta có: \(BD<\frac{a+b+c+d}{2}\)

Từ đó suy ra \(AC+BD<a+b+c+d\).