25 bài tập vận dụng Hình thang, hình thang cânLàm bàiQuảng cáo
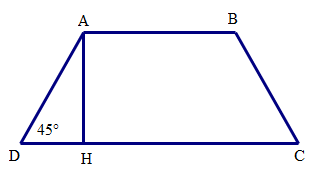
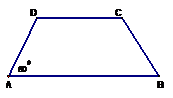
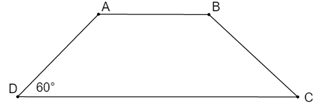
Câu hỏi 1 : Cho hình thang cân \(ABCD\) có đáy nhỏ \(AB = 4cm\), đường cao \(AH = 6cm\), và \(\widehat D = {45^0}\). Độ dài đáy lớn \(CD\) bằng
Đáp án: B Phương pháp giải: Lời giải chi tiết: Hướng dẫn giải chi tiết
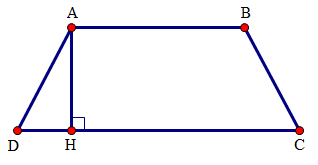
Ta có tam giác \(ADH\) vuông cân tại \(D\) vì \(\widehat{D}={{45}^{0}}\). Do đó \(DH = AH = 6 cm\) Mà \(DH =DH=\dfrac{1}{2}\left( CD-AB \right)\) Suy ra \(CD = 2DH + AB = 12 + 4 = 16 (cm) \) Vậy \(CD = 16cm\). Chọn B Câu hỏi 2 : Cho hình thang cân \(ABCD (AB // CD)\) đáy nhỏ \(AB = 8 cm\), đáy lớn \(CD = 12 cm\). Kẻ đường cao \(AH\). Độ dài \(DH\) bằng:
Đáp án: A Phương pháp giải: Lời giải chi tiết: Hướng dẫn giải chi tiết
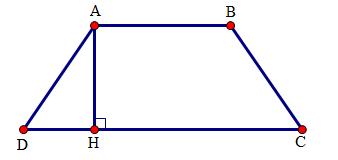
Ta có \(DH=\dfrac{1}{2}\left( CD-AB \right)\) \(DH = DH=\dfrac{1}{2}\left( 12-8 \right)=2\,\,cm\) Vậy \(DH = 2cm\) Chọn A. Câu hỏi 3 : Cho hình thang cân \(ABCD\) đáy nhỏ \(AB = 4 cm\), đáy lớn \(CD = 10 cm\), cạnh bên \(BC = 5cm\) thì đường cao \(AH\) bằng:
Đáp án: B Phương pháp giải: Lời giải chi tiết: Hướng dẫn giải chi tiết
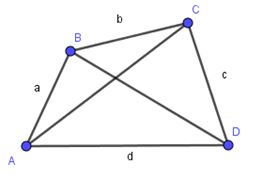
Ta có \(DH=\dfrac{1}{2}\left( CD-AB \right)=\dfrac{1}{2}\left( 10-4 \right)=3\,\,cm\) Do \(ABCD\) là hình thang cân nên \(AD = BC = 5cm\) Áp dụng định lý Pi – ta – go vào tam giác \(ADH\) vuông tại \(H\) ta có: \(\begin{array}{l}A{D^2} = A{H^2} + D{H^2}\\A{H^2} = A{D^2} - D{H^2}\\A{H^2} = {5^2} - {3^2}\\AH = 4\end{array}\) Vậy \(AH = 4 cm\). Chọn B. Câu hỏi 4 : Cho hình thang \(ABCD\), trong đó \(\hat C + \hat D = 150^\circ \) . Tổng số đo của \(\hat A + \hat B\) là:
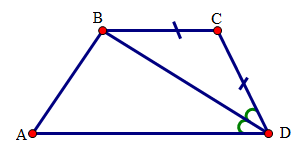
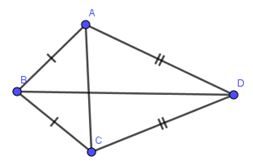
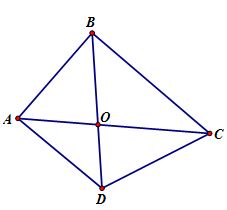
Đáp án: C Phương pháp giải: Lời giải chi tiết: Hướng dẫn giải chi tiết: Trong hình thang \(ABCD\) có: \(\hat A + \hat B = {360^0} - \left( {\hat C + \hat D} \right) = {360^0} - {150^0} = {210^0}\) Chọn C. Câu hỏi 5 : (1 điểm) Cho tứ giác \(ABCD\) có \(BC = CD\) và \(DB\) là tia phân giác của góc \(D\). Chứng minh rằng \(ABCD\) là hình thang.
Đáp án: A Phương pháp giải: Lời giải chi tiết: Hướng dẫn giải chi tiết:
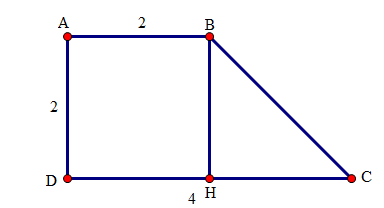
Xét \(\Delta BCD\) có \(BC = CD(gt)\) nên \(\Delta BCD\) là tam giác cân. Suy ra \(\widehat {CBD} = \widehat {CDB}\) Vì \(DB\) là tia phân giác góc \(D\) của tứ giác \(ABCD\) nên \)\widehat {ADB} = \widehat {CDB}\) Do đó \(\widehat {CBD} = \widehat {ADB}\) Mà hai góc \(\widehat {CBD}\) và \(\widehat {ADB}\) là hai góc ở vị trí so le trong nên suy ra \(BC//AD\) . Tứ giác \(ABCD\) có \(AD//BC\) (cmt) nên là hình thang. Câu hỏi 6 : (1 điểm) Cho hình thang vuông \(ABCD\) có \(\hat A = \hat D = 90^\circ ,\;AB = AD = 2cm,\;DC = 4cm\) . Tính các góc của hình thang.
Đáp án: D Phương pháp giải: Lời giải chi tiết: Hướng dẫn giải chi tiết:
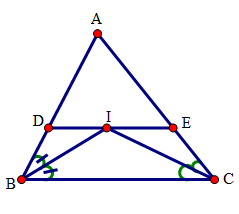
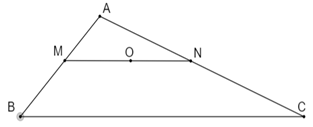
Từ \(B\) kẻ \(BH\) vuông góc với \(CD\). Tứ giác \(ABHD\) có \(\widehat A = {90^0},\widehat D = {90^0},\widehat H = {90^0}\) (gt) nên là hình chữ nhật. Do đó \(AD = BH,AB = DH\) . Mặt khác, \(AB = AD = 2cm\) nên suy ra \(BH = DH = 2cm\) . Do đó: \(HC = DC - HD = 4 - 2 = 2cm\) . Tam giác \(BHC\) có \(BH = HC = 2cm\) nên tam giác \(BHC\) cân đỉnh \(H\). Lại có \(\widehat {BHC} = 90^\circ \) (do cách vẽ) nên tam giác \(BHC\) vuông cân tại \(H\). Do đó \(\widehat {BCH} = \left( {180^\circ - \widehat {BHC}} \right):2 = \left( {180^\circ - 90^\circ } \right):2 = 45^\circ \) Xét hình thang \(ABCD\) có: \(\widehat {ABC} = 360^\circ - \left( {\hat A + \hat D + \hat C} \right) = 360^\circ - \left( {90^\circ + 90^\circ + 45^\circ } \right) = 135^\circ \) Câu hỏi 7 : (2 điểm) Cho tam giác \(ABC\). Các tia phân giác của các góc \(B\) và \(C\) cắt nhau tại \(I\). Qua \(I\) kẻ đường thẳng song song với \(BC\), cắt các cạnh \(AB,AC\) lần lượt tại \(D\) và \(E\). a) Chứng minh các tứ giác \(BDIC,BIEC,BDEC\) là hình thang b) Chứng minh: \(DE = BD + CE\) .
Đáp án: B Phương pháp giải: Lời giải chi tiết: Hướng dẫn giải chi tiết:
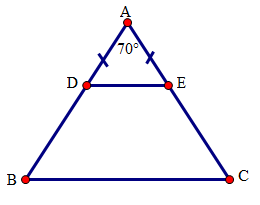
a) Xét tứ giác \(DECB\) có: \(DE//BC\) (gt) nên tứ giác \(DECB\) là hình thang. Tương tự : Tứ giác \(DICB\) có \(DI//BC\) (gt) nên tứ giác \(DICB\) là hình thang Tứ giác \(IECB\) có \(IE//CB\) (gt) nên tứ giác \(IECB\) là hình thang. b) Ta sẽ chứng minh: \(DE = BD + CE\) . Thật vậy, Vì \(DE//BC\) (gt) nên suy ra \(\widehat {DIB} = \widehat {IBC}\) ( so le trong) Mà \(\widehat {DBI} = \widehat {IBC}\) (gt) nên \(\widehat {DIB} = \widehat {DBI}\) Suy ra tam giác \(BDI\) cân đỉnh \(D\). Do đó \(DI = DB(1)\) Ta có: \(IE//CB\) nên suy ra \(\widehat {EIC} = \widehat {BCI}\) ( so le trong) Mà \(\widehat {BCI} = \widehat {ECI}\) (gt) nên \(\widehat {ECI} = \widehat {EIC}\) Suy ra tam giác \(EIC\) cân đỉnh \(E\). Do đó \(EI = EC(2)\). Cộng (1) và (2) vế theo vế ta được: \(DI + EI = BD + CE \Rightarrow DE = BD + CE\) Vậy hình thang \(BDEC\) có một cạnh đáy bằng tổng hai cạnh bên. Câu hỏi 8 : (1 điểm) Cho tam giác \(ABC\) cân tại \(A\). Gọi \(D,E\) theo thứ tự thuộc các cạnh bên \(AB,AC\) sao cho \(AD{\text{ }} = {\text{ }}AE\) . a) Tứ giác \(BDEC\) là hình gì? Vì sao? b) Tính các góc của hình thang \(BEDC\) , biết \(A = {70^o}\) .
Đáp án: A Phương pháp giải: Lời giải chi tiết: Hướng dẫn giải chi tiết:
a) Tam giác \(ADE\) có \(AD = AE(gt)\) nên tam giác \(ADE\) cân tại \(A\). Suy ra \(\widehat {ADE} = \widehat {AED} = \left( {180^\circ - \widehat {DAE}} \right):2\;\left( 1 \right)\) Tam giác \(ABC\) cân tại \(A\) (gt) nên \(\widehat {ABC} = \widehat {ACB} = \left( {180^\circ - \widehat {BAC}} \right):2\;\;\;\;\left( 2 \right)\) Từ (1) và (2) suy ra \(\widehat {ADE} = \widehat {ABC}\) Mà 2 góc \(\widehat {ADE}\) và \(\widehat {ABC}\) là hai góc ở vị trí đồng vị nên suy ra \(DE\parallel BC\) Tứ giác \(BDEC\) có \(DE // BC\) nên tứ giác \(BDEC\) là hình thang b) Ta có : \(\hat A = 70^\circ \) Theo ý a) suy ra: \(\begin{array}{l}\widehat {ADE} = \widehat {AED}\widehat { = ABC} = \widehat {ACB} = \left( {180^\circ - \widehat {DAE}} \right):2\\ = (180^\circ - 70^\circ ):2\\ = 55^\circ \;\;\;\;\;\;\;\;\;\;\;\;\;\end{array}\) Vì \(\widehat {BDE}\) và \(\widehat {ADE}\) là hai góc kề bù nên \(\widehat {BDE} = 180^\circ - \widehat {ADE} = 180^\circ - 55^\circ = 125^\circ \) Mặt khác,\(\widehat {DEA}\) và \(\widehat {DEC}\) là hai góc kề bù nên \(\widehat {DEC} = 180^\circ - \widehat {DEA} = 180^\circ - 55^\circ = 125^\circ \) Câu hỏi 9 : Một hình thang cân có cạnh bên là 2,5cm; đường trung bình là 3cm. Chu vi của hình thang là:
Đáp án: D Phương pháp giải: + Dựa vào tính chất của hình thang cân suy ra hai cạnh bên bằng nhau và bằng 2,5cm. + Tổng độ dài hai đáy bằng hai lần độ dài đường trung bình + Tổng độ dài hai đáy và độ dài hai cạnh bên là chu vi hình thang cân cần tìm. Lời giải chi tiết: Tổng độ dài hai đáy là: \(3.2=6(cm)\) Chu vi hình thang là: \(2,5.2+6=11(cm)\) Chọn D. Câu hỏi 10 : Cho tứ giác ABCD có \(\widehat{A\,\,}=65{}^\circ ~;\,\,\widehat{B\,\,}=117{}^\circ ;\,\,\widehat{C\,\,}=71{}^\circ .\) Tính số đo góc ngoài đỉnh D.
Đáp án: A Phương pháp giải: Lời giải chi tiết: \(\widehat{CDx}\) là góc ngoài đỉnh D. Tứ giác ABCD có: \(\widehat{D\,}=360{}^\circ -\left( \widehat{A\,\,}+\widehat{B\,\,}+\widehat{C\,\,} \right)=360{}^\circ -\left( 65{}^\circ +117{}^\circ +71{}^\circ \right)=107{}^\circ \). Vì \(\widehat{ADC}\) và \(\widehat{CDx}\) là hai góc kề bù nên \(\widehat{CDx}=180{}^\circ -\widehat{D\,}=180{}^\circ -107{}^\circ =73{}^\circ \) Câu hỏi 11 : Cho tứ giác ABCD có\(AB=BC,~CD=DA\). a) Chứng minh rằng BD là đường trung trực của AC. b) Cho biết \(\widehat{B\,\,}=100{}^\circ ~;\,\,\widehat{D\,\,}=70{}^\circ \) Tính \(\widehat{A\,\,};\,\,\widehat{C\,\,}\) .
Đáp án: C Phương pháp giải: Lời giải chi tiết: a) Ta có: \(BA=BC(gt);DA=DC(gt)\) nên BD là đường trung trực của AC. (đpcm) b) Xét \(\Delta ABD\) và \(\Delta CBD\) có: \(\begin{align}& BA=BC(gt) \\ & DA=DC(gt) \\ \end{align}\) \(BD\) cạnh chung Suy ra \(\Delta ABD=\Delta CBD\) (c.c.c) Suy ra \(\widehat{BAD}=\widehat{BCD}\) ( hai góc tương ứng) Ta lại có: \(\widehat{BAD}+\widehat{BCD}=360{}^\circ -\widehat{B\,\,}-\widehat{D\,\,}=360{}^\circ -100{}^\circ -70{}^\circ =190{}^\circ \) Do đó: \(\widehat{BAD}=\widehat{BCD}=190{}^\circ :2=95{}^\circ \) Câu hỏi 12 : Tứ giác ABCD có \(\widehat{A\,\,}=110{}^\circ ;\,\,\widehat{B\,\,}=100{}^\circ \) . Các tia phân giác của các góc C và D cắt nhau tại E. Các đương phân giác của các góc ngoài tại đỉnh C và D cắt nhau tại F. Tính \(\widehat{CED};\,\,\,\widehat{CFD}\).
Đáp án: B Phương pháp giải: Lời giải chi tiết:
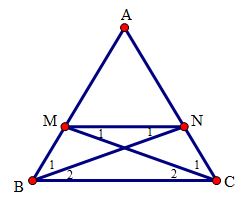
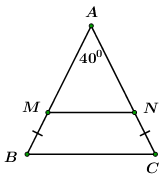
Tứ giác ABCD có: \(\widehat{C\,\,}+\widehat{D\,\,}=360{}^\circ -\widehat{A\,\,}-\widehat{B\,\,}=360{}^\circ -110{}^\circ -100{}^\circ =150{}^\circ \) Nên \(\widehat{ECD}+\widehat{EDC}=\left( \widehat{C\,\,}+\widehat{D\,\,} \right):2=150{}^\circ :2=75{}^\circ \) Xét \(\Delta CED\) có: \(\widehat{CED}=180{}^\circ -\left( \widehat{ECD}+\widehat{EDC} \right)=180{}^\circ -75{}^\circ =105{}^\circ \) Vì DE và DF là các tia phân giác của hai góc kề bù nên \(DE\bot DF\) . Tương tự ta có: \(CE\bot CF\) . Xét tứ giác CEDF có: \(\widehat{F\,\,}=360{}^\circ -\widehat{E\,\,}-\widehat{ECF}-\widehat{EDF}=360{}^\circ -105{}^\circ -90{}^\circ -90{}^\circ =75{}^\circ \) Câu hỏi 13 : Cho tam giác ABC cân tại A. Trên các cạnh bên AB, AC lấy các điểm M, N sao cho BM = CN. a) Tứ giác BMNC là hình gì? Vì sao? b) Tính các góc của tứ giác BMNC biết \(\widehat{A}={{40}^{\circ }}\)? c) Các điểm M, N ở vị trí nào để BM = MN = NC?
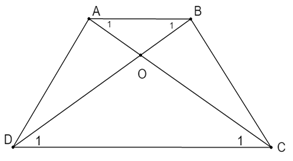
Đáp án: A Phương pháp giải: Lời giải chi tiết: a) Ta có: AB = AM + MB AC = AN + NC Mà AB = AC (do tam giác ABC cân tại A) BM = NC ( gt) Suy ra AN = AM Xét tam giác AMN có: AM = AN (cmt) Suy ra tam giác AMN cân tại A. Suy ra \(\widehat{AMN}=\widehat{ANM}\) Xét tam giác ANM có: \(\widehat{A}+\widehat{AMN}+\widehat{ANM}={{180}^{0}}\) (tổng ba góc trong một tam giác) \(\widehat{AMN}=\frac{{{180}^{0}}-\widehat{A}}{2}\) ( vì \(\widehat{AMN}=\widehat{ANM}\) ) (1) Xét tam giác ABC cân tại A ta có: \(\widehat{A}+\widehat{B}+\widehat{C}={{180}^{0}}\) (tổng ba góc trong một tam giác) \(\widehat{B}=\frac{{{180}^{0}}-\widehat{A}}{2}\) ( vì \(\widehat{B}=\widehat{C}\)) (2) Từ (1) và (2) \(\widehat{AMN}=\widehat{B}\) Mà \(\widehat{AMN},\widehat{B}\) là hai góc đồng vị nên MN // BC. Xét tứ giác MNCB có MN // BC nên MNCB là hình thang. Lại có \(\widehat{B}=\widehat{C}\) (\(\Delta ABC\) cân tại A) nên MNCB là hình thang cân. b. Ta có \(\widehat{B}=\frac{{{180}^{0}}-\widehat{A}}{2}=\frac{{{180}^{0}}-{{40}^{0}}}{2}={{70}^{0}}\) Ta có : \(\widehat{B}+\widehat{BMN}={{180}^{0}}\) (hai góc trong cùng phía) \(\widehat{BMN}={{180}^{0}}-\widehat{B}={{180}^{0}}-{{70}^{0}}={{110}^{0}}\) Do \(BMNC\) là hình thang cân nên \(\widehat{BMN}=\widehat{MNC}={{110}^{0}}\), \(\widehat{B}=\widehat{C}={{70}^{0}}\) Vậy \(\widehat{BMN}=\widehat{MNC}={{110}^{0}}\), \(\widehat{B}=\widehat{C}={{70}^{0}}\). c. Ta có BM = MN khi và chỉ khi \(\widehat{{{N}_{1}}}=\widehat{{{B}_{1}}}={{70}^{0}}\) \(\Leftrightarrow \widehat{{{B}_{1}}}=\widehat{{{B}_{2}}}\) (vì \(\widehat{{{N}_{1}}}=\widehat{{{B}_{2}}}\)) Tương tự MN = NC khi và chỉ khi \(\widehat {{M_1}} = \widehat {{C_1}} \Leftrightarrow \widehat {{C_1}} = \widehat {{C_2}}\,\,\,\left( {do\,\,\,\widehat {{M_1}} = \widehat {{C_2}}} \right)\) Như vậy, nếu BN và CM là các đường phân giác của tam giác ABC thì BM = MN = CN. Câu hỏi 14 : Cho hình thang cân ABCD (AB // CD) có hai đường chéo cắt nhau tại I, hai đường thẳng chứa các cạnh bên cắt nhau ở K. Chứng minh rằng KI là đường trung trực của hai đáy. Phương pháp giải: Lời giải chi tiết: Xét tam giác ACD và tam giác BDC có: AD = BC (do ABCD là hình thang cân) AC= BD (do ABCD là hình thang cân) CD là cạnh chung Suy ra \(\Delta ACD=\Delta BDC\)(c.c.c). Suy ra \(\widehat{ACD}=\widehat{BDC}\) (hai góc tương ứng). Xét tam giác ICD có \(\widehat{ACD}=\widehat{BDC}\)(cmt), suy ra tam giác ICD cân tại I. Do đó ID = IC (1) Tam giác KCD có hai góc ở đáy bằng nhau nên tam giác KCD cân ở K. Do đó KC = KD (2) Từ (1) và (2) suy ra KI là đường trung trực của CD (*) Xét tam giác ADB và tam giác BCA có: AD = BC (cmt) AB là cạnh chung AC = BD Suy ra \(\Delta ADB=\Delta BCA\)(c.c.c). Suy ra \(\widehat{ABD}=\widehat{BAC}\) . Xét tam giác IAB có \(\widehat{ABD}=\widehat{BAC}\) nên tam giác IAB cân tại I. Do đó IA = IB (3) Ta có: KA = KD – AD ; KB = KC – BC . Mà KD = KC, AD = BC, do đó KA = KB (4) Từ (3) và (4) suy ra KI là đường trung trực của AB. (**) Từ (*) và (**) suy ra KI là đường trung trực của hai đáy (đpcm)
Câu hỏi 15 : Cho hình thang cân \(ABCD (AB // CD)\). Có góc \(BAD\) bằng \({60^0}\) . Số đo góc \(C\) bằng:
Đáp án: C Phương pháp giải: Lời giải chi tiết: Hướng dẫn giải chi tiết
Ta có \(\widehat{D}+\widehat{A}={{180}^{0}}\) \(\begin{array}{l} \Rightarrow \widehat D = {180^0} - \widehat A\\\,\,\,\,\,\,\,\,\,\,\,\,\, = {180^0} - {60^0}\\\,\,\,\,\,\,\,\,\,\,\,\,\, = {120^0}\end{array}\) Do \(ABCD\) là hình thang cân nên \(\widehat{D}=\widehat{C}={{120}^{0}}\) Vậy \(\widehat{C}={{120}^{0}}\) Chọn C Câu hỏi 16 : Cho hình thang cân ABCD (AB//CD) có AD = 4cm; \(\angle {\rm{B}} = 120^\circ \). Chọn ý đúng:
Đáp án: D Phương pháp giải: Hình thang cân là hình thang có hai cạnh bên bằng nhau và hai cạnh bên bằng nhau, hai đường chéo bằng nhau. Lời giải chi tiết: Ta có ABCD (AB//CD) là hình thang cân nên \(\angle {\rm{A}} = \angle {\rm{B}} = 120^\circ ;\) \(\angle {\rm{C}} = \angle {\rm{D}}\,\,\left( 1 \right)\) Mà \(\angle {\rm{A}} + \angle {\rm{B}} + \angle {\rm{C}} + \angle {\rm{D}} = 360^\circ \) \( \Rightarrow \angle {\rm{C}} + \angle {\rm{D}} = {\rm{36}}0^\circ - 2\angle {\rm{B}}\) \( = {\rm{36}}0^\circ - 2.120^\circ = 120^\circ \,\,\,\,\left( 2 \right)\) Từ (1), (2) ta kết luận \(\angle {\rm{C}} = \angle {\rm{D}} = 60^\circ \) Chọn D. Câu hỏi 17 : Tìm số đo góc B, biết tứ giác ABCD (AB//CD) là hình thang cân và \(\angle {\rm{D}} = 60^\circ \)
Đáp án: C Phương pháp giải: Hình thang cân là hình thang có hai góc kề đáy bằng nhau. Lời giải chi tiết: Ta có ABCD là hình thang cân nên \(\angle {\rm{A}} = \angle {\rm{B}}\,\,\,\left( 1 \right)\) (tính chất hình thang cân) Mà \(\angle {\rm{A}} + \angle {\rm{B}} + \angle {\rm{C}} + \angle {\rm{D}} = 360^\circ \) \( \Rightarrow \angle {\rm{A}} + \angle {\rm{B}} = {360^0} - \left( {\angle C + \angle D} \right)\) \( = {360^0} - {2.60^0} = 240^\circ \,\,\,\,\left( 2 \right)\) Từ (1), (2) ta kết luận \(\angle {\rm{A = }}\angle {\rm{B}} = 120^\circ \) Chọn C. Câu hỏi 18 : Cho tam giác ABC. Từ điểm O trong tam giác đó kẻ đường thẳng song song với BC cắt cạnh AB ở M, cắt cạnh AC ở N. a) Tứ giác BMNC là hình gì? Vì sao? b) Tìm điều kiện của DABC để tứ giác BMNC là hình thang cân? Phương pháp giải: Áp dụng định nghĩa của hình thang: hình thang là tứ giác có 2 cạnh đối song song. Áp dụng định nghĩa của hình thang cân: hình thang cân là hình thang có 2 góc kề một đáy bằng nhau Lời giải chi tiết: a) Tứ giác BMNC là hình gì? Vì sao? Theo đề bài ta có: \(MN//BC.\) \( \Rightarrow BMNC\) là hình thang. (định nghĩa) b) Tìm điều kiện của DABC để tứ giác BMNC là hình thang cân? Theo câu a) ta có: \(BMNC\) là hình thang có hai đáy \(MN,\,\,BC.\) \( \Rightarrow BMNC\) là hình thang cân \( \Leftrightarrow \angle B = \angle C.\) \( \Rightarrow \Delta ABC\) là tam giác cân tại \(A.\) Vậy để \(BMNC\) là hình thang cân thì \(\Delta ABC\) là tam giác cân tại \(A.\) Câu hỏi 19 : Cho tam giác ABC cân tại A. Trên các cạnh AB, AC lấy các điểm M, N sao cho BM = CN a) Tứ giác BMNC là hình gì ? vì sao ? b) Tính các góc của tứ giác BMNC biết rằng \(\angle {\rm{A}} = 40^\circ \) Phương pháp giải: Áp dụng định nghĩa của hình thang: hình thang là tứ giác có 2 cạnh đối song song Áp dụng định nghĩa của hình thang cân: hình thang cân là hình thang có 2 góc kề một đáy bằng nhau Lời giải chi tiết: a) Tứ giác BMNC là hình gì ? Vì sao ? Theo đề bài ta có: \(\Delta ABC\) cân tại \(A\) \( \Rightarrow AB = AC\) và \(\angle B = \angle C = \frac{{{{180}^0} - \angle A}}{2}.\) Ta có: \(\left\{ \begin{array}{l}AB = AM + BM\\AC = AN + NC\end{array} \right.\) Mà \(BM = NC\,\,\left( {gt} \right) \Rightarrow AM = AN\) (tính chất bắc cầu). \( \Rightarrow \Delta AMN\) cân tại \(A\) \( \Rightarrow \angle AMN = \angle ANM = \frac{{{{180}^0} - \angle A}}{2}.\) \( \Rightarrow \angle AMN = \angle B = \frac{{{{180}^0} - \angle A}}{2}\) Mà hai góc này là hai góc đồng vị \( \Rightarrow MN//BC \Rightarrow BMNC\) là hình thang. (định nghĩa) Lại có: \(\angle B = \angle C\,\,\,\left( {cmt} \right)\) \( \Rightarrow BMNC\) là hình thang cân. (dhnb) b) Tính các góc của tứ giác BMNC biết rằng \(\angle {\rm{A}} = 40^\circ \) Ta có: \(\angle B = \angle C = \frac{{{{180}^0} - \angle A}}{2} = \frac{{{{180}^0} - {{40}^0}}}{2} = {70^0}.\) Lại có: \(\angle BMN + \angle MNC + \angle B + \angle C = {360^0}\) (tổng các góc trong hình thang) \( \Rightarrow \angle BMN + \angle MNC = {360^0} - 2\angle B = {360^0} - {70^0}.2 = {220^0}\) \( \Rightarrow \angle BMN = \angle MNC = \frac{{{{220}^0}}}{2} = {110^0}.\) (do \(BMNC\) là hình thang cân). Câu hỏi 20 : Cho hình thang ABCD (AB//CD) có O là giao điểm hai đường chéo AC và BD. Chứng minh rằng: ABCD là hình thang cân nếu OA = OB Phương pháp giải: Áp dụng định nghĩa của hình thang: hình thang là tứ giác có 2 cạnh đối song song. Áp dụng định nghĩa của hình thang cân: hình thang cân là hình thang có 2 góc kề một đáy bằng nhau. Áp dụng các tính chất của hình thang cân: hình thang cân có 2 cạnh bên bằng nhau, 2 đường chéo bằng nhau. Lời giải chi tiết: Theo đề bài ta có: ABCD là hình thang có hai đáy AB, CD. Lại có: \(OA = OB \Rightarrow \Delta OAB\) cân tại \(O.\) \( \Rightarrow \angle {A_1} = \angle {B_1}\) (tính chất tam giác cân). Mà \(AB//CD\) \( \Rightarrow \left\{ \begin{array}{l}\angle {A_1} = \angle {C_1}\\\angle {B_1} = \angle {D_1}\end{array} \right.\) (các cặp góc so le trong) \( \Rightarrow \angle {C_1} = \angle {D_1}\,\,\left( { = \angle {A_1}} \right)\) \( \Rightarrow \Delta OCD\) cân tại \(O.\) (định nghĩa). \( \Rightarrow OA + AC = OB + OD \Leftrightarrow AC = BD.\) \( \Rightarrow ABCD\) là hình thang cân. (dhnb) Câu hỏi 21 : Chứng minh rằng trong một tứ giác, tổng hai đường chéo lớn hơn tổng hai cạnh đối. Phương pháp giải: Lời giải chi tiết: Gọi O là giao điểm của hai đường chéo AC, BD của tứ giác ABCD. Xét tam giác AOB có: \(OA+OB>AB\) ( quan hệ giữa ba cạnh của tam giác) Xét tam giác COD có: \(OC+OD>CD\) ( quan hệ giữa ba cạnh của tam giác) Suy ra: \(\begin{align}& OA+OB+OC+OD>AB+CD \\ & \Leftrightarrow AC+BD>AB+CD \\ \end{align}\) Tương tự: \(AC+BD>AD+BC\) Vậy trong một tứ giác, tổng hai đường chéo lớn hơn tổng hai cạnh đối.
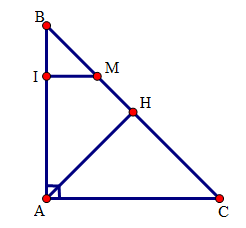
Câu hỏi 22 : Chứng minh rằng trong một tứ giác, tổng hai đường chéo lớn hơn nửa chu vi nhưng nhỏ hơn chu vi của tứ giác ấy. Phương pháp giải: Lời giải chi tiết: Đặt \(AB=a,BC=b,CD=c,DA=d\) . Áp dụng kết quả câu 4 ta có: \(AC+BD>a+c\) \(AC+BD>b+d\) Do đó: \(2\left( AC+BD \right)>a+b+c+d\) Suy ra \(AC+BD>\frac{a+b+c+d}{2}\) . Xét tam giác ABC có: \(AC<a+b\) . Xét tam giác ADC có: \(AC<c+d\). Do đó: \(2AC<a+b+c+d\) Suy ra: \(AC<\frac{a+b+c+d}{2}\) Tương tự ta có: \(BD<\frac{a+b+c+d}{2}\) Từ đó suy ra \(AC+BD<a+b+c+d\). Câu hỏi 23 : (2 điểm) Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\). Trên \(BC\) lấy điểm \(M\) sao cho \(CM = CA\) . Đường thẳng đi qua \(M\) và song song với \(CA\) cắt \(AB\) tại \(I\). a) Tứ giác \(ACMI\) là hình gì ? b) So sánh \(AB + AC\) và \( AH + BC\) .
Đáp án: D Phương pháp giải: Lời giải chi tiết: Hướng dẫn giải chi tiết:
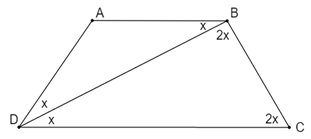
a) Tứ giác \(ACMI\) có \(MI//AC\left( {gt} \right)\) và \(\hat A = 90^\circ (gt)\) nên là hình thang vuông. b) Xét tam giác \(AMC\) có \(CM = AC(gt)\) nên tam giác \(AMC\) cân tại \(C\). Suy ra \(\widehat {MAC} = \widehat {AMC}(1)\) Xét tam giác \(AMH\) có : \(\widehat {MAH} = 90^\circ \widehat { - AMH}\) (hai góc phụ nhau)(2) Xét tam giác \(ABC\) vuông tại \(A\): \(\widehat {MAB} = \widehat {BAC} - \widehat {MAC} = 90^\circ - \widehat {MAC}\) (phụ nhau)(3) Từ (1),(2) và (3) suy ra: \(\widehat {MAH} = \widehat {MAB} \Rightarrow \widehat {MAH} = \widehat {MAI}\) Xét hai tam giác vuông \(\Delta AHM\) và \(\Delta AIM\) có: \(AM\) cạnh chung \(\widehat {MAH} = \widehat {MAI}\) (cmt) \( \Rightarrow \;\Delta AHM = \Delta AIM\) ( cạnh huyền-góc nhọn) \( \Rightarrow AH = AI\) ( hai cạnh tương ứng) Lại có: \(MI\parallel AC(gt),AC \bot AB(gt) \Rightarrow MI \bot AB\) Do đó \(BI < BM(4)\) ( quan hệ giữa đường vuông góc và đường xiên) Mặt khác: \(AC = CM(gt)(5)\) \(AI = AH(cmt)(6)\) Cộng (6),(4),(5) vế theo vế ta được: \(AI + BI + AC < AH + BM + CM\) \( \Rightarrow AB + AC < AH + BC\) Vậy ta có điều phải chứng minh. Câu hỏi 24 : Cho hình thang cân ABCD (AB // DC) có AB < DC. Chứng minh rằng : DC – AB < 2AD Phương pháp giải: Lời giải chi tiết: Gọi E là điểm trên cạnh DC sao cho CE = AB. Xét tam giác ABC và tam giác CEA có: AB = CE (gt) \(\widehat{BAC}=\widehat{ECA}\) (so le trong) AC là cạnh chung Suy ra \(\Delta ABC=\Delta CEA\) (c.g.c) Suy ra BC = AE (hai cạnh tương ứng) Ta có AD = BC (do ABCD là hình thang cân) Suy ra AD = AE Xét tam giác ADE có : DE < AD +AE (bất đẳng thức tam giác) Suy ra DC – CE < AD + AD ( do AD = AE) Suy ra DC – AB < 2AD Vậy DC – AB < 2AD (đpcm) Câu hỏi 25 : Hình thang cân ABCD (AB//CD) có đường chéo BD chia hình thang thành hai tam giác cân: tam giác ABD cân tại A và tam giác BCD cân tại D. Tính các góc của hình thang cân đó.
Đáp án: A Phương pháp giải: Áp dụng định nghĩa của hình thang: hình thang là tứ giác có 2 cạnh đối song song Áp dụng định nghĩa của hình thang cân: hình thang cân là hình thang có 2 góc kề một đáy bằng nhau Áp dụng các tính chất của hình thang cân: hình thang cân có 2 cạnh bên bằng nhau, 2 đường chéo bằng nhau Lời giải chi tiết: Đặt \(\angle ADB = x\,\,\left( {0^\circ < x < 90^\circ } \right)\). Ta có: \(\Delta ADB\) cân tại \(A \Rightarrow \angle ADB = \angle ABD = x.\) Mà \(AB//CD \Rightarrow \angle ABD = \angle BDC = x\) (hai góc so le trong) \( \Rightarrow \angle ADC = \angle ADB + \angle BDC = x + x = 2x.\) Lại có: \(ABCD\) là hình thang cân \( \Rightarrow \angle ADC = \angle DCB = 2x\) Mà \(\Delta BDC\) cân tại\(D\,\,\left( {gt} \right) \Rightarrow \angle DBC = \angle DCB = 2x\) Xét \(\Delta BDC\) ta có: \(\angle BDC + 2\angle DCB = {180^0}\) \( \Leftrightarrow x + 2.2x = {180^0} \Leftrightarrow 5x = {180^0} \Leftrightarrow x = {36^0}.\) \( \Rightarrow \angle ADC = \angle DCB = 2.36 = {72^0}.\) \( \Rightarrow \angle DAB = \angle ABC = \frac{{{{360}^0} - 2\angle ADC}}{2}\) \( = \frac{{{{360}^0} - {{2.72}^0}}}{2} = {108^0}.\) Vậy hình thang \(ABCD\) có các góc là:\(\angle A = \angle B = {108^0},\,\,\angle C = \angle D = {72^0}.\) Chọn B. Quảng cáo
|