Câu hỏi:
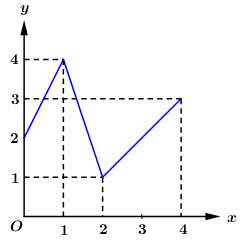
Một vật chuyển động trong 4 giờ có đồ thị vận tốc v \(\left( {km/h} \right)\) phụ thuộc thời gian t \(\left( h \right)\) có đồ thị vận tốc như hình vẽ bên. Tính quãng đường\(s\)mà vật đi được trong 4 giờ đó.
- A \(9,5\left( {km} \right)\)
- B \(19\left( {km} \right)\)
- C \(15\left( {km} \right)\)
- D \(7,5\left( {km} \right)\)
Phương pháp giải:
- Tìm hàm vận tốc trong từng khoảng thời gian cụ thể.
- Áp dụng công thức \(s = \int {vdt} \).
Lời giải chi tiết:
Trong 1h đầu tiên, đồ thị hàm vận tốc là đường thẳng đi qua các điểm \(\left( {0;2} \right);\,\,\left( {1;4} \right)\).
\( \Rightarrow \) Phương trình hàm số vận tốc trong 1 giây đầu tiên là: \(\dfrac{{x - 0}}{{1 - 0}} = \dfrac{{v - 2}}{{4 - 2}} \Leftrightarrow v = 2x + 2\).
Trong giờ thứ nhất đến giờ thứ 2, đồ thị hàm vận tốc là đường thẳng đi qua các điểm \(\left( {1;4} \right),\,\,\left( {2;1} \right)\).
\( \Rightarrow \) Phương trình hàm số vận tốc trong giờ thứ nhất đến giờ thứ 2 là: \(\dfrac{{x - 1}}{{2 - 1}} = \dfrac{{v - 4}}{{1 - 4}} \Leftrightarrow v = - 3x + 7\).
Trong giờ thứ 2 đến giờ thứ 4, đồ thị hàm vận tốc là đường thẳng đi qua các điểm \(\left( {2;1} \right),\,\,\left( {4;3} \right)\).
\( \Rightarrow \) Phương trình hàm số vận tốc trong giờ thứ 2 đến giờ thứ 4 là: \(\dfrac{{x - 2}}{{4 - 2}} = \dfrac{{v - 1}}{{3 - 1}} \Leftrightarrow v = x - 1\).
Vậy quãng đường vật đã đi trong 4 giờ là
\(\begin{array}{l}s = \int\limits_0^1 {\left( {2x + 2} \right)dx} + \int\limits_1^2 {\left( { - 3x + 7} \right)dx} + \int\limits_2^4 {\left( {x - 1} \right)dx} \\\,\,\, = 3 + 2,5 + 4 = 9,5\,\,\,\left( {km} \right)\end{array}\)
Chọn A.


















