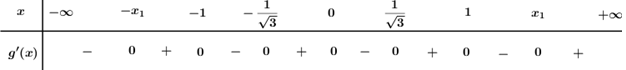Câu hỏi:
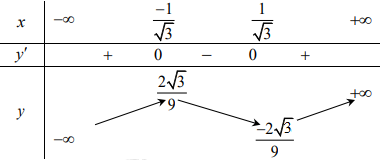
Cho hàm số \(y = f\left( x \right) = {x^3} + a{x^2} + bx + c\), \(a,\,\,b,\,\,c \in \mathbb{R}\) có bảng biến thiên như hình vẽ dưới đây.
Gọi \(F\left( x \right)\) là một nguyên hàm của \(f\left( x \right)\). Hàm số \(g\left( x \right) = F\left( {f\left( x \right)} \right)\) nghịch biến trên khoảng nào dưới đây?
- A \(\left( { - \infty ; + \infty } \right)\)
- B \(\left( { - \infty ;2} \right)\)
- C \(\left( { - \infty ; - 2} \right)\)
- D \(\left( { - 2;2} \right)\)
Phương pháp giải:
Lời giải chi tiết:
Ta có \(f'\left( x \right) = 3{x^2} + 2ax + b\).
Dựa vào BBT ta thấy phương trình \(f'\left( x \right) = 0\) có 2 nghiệm \(x = \pm \dfrac{1}{{\sqrt 3 }}\) nên
\(f'\left( x \right) = 3\left( {x + \dfrac{1}{{\sqrt 3 }}} \right)\left( {x - \dfrac{1}{{\sqrt 3 }}} \right) = 3\left( {{x^2} - \dfrac{1}{3}} \right) = 3{x^2} - 1\).
Đồng nhất hệ số ta có \(a = 0,\,\,b = - 1\), khi đó hàm số có dạng \(y = {x^3} - x + c\).
Đồ thị hàm số đi qua điểm \(\left( { - \dfrac{1}{{\sqrt 3 }};\dfrac{{2\sqrt 3 }}{9}} \right)\) nên ta có \(\dfrac{{2\sqrt 3 }}{9} = {\left( { - \dfrac{1}{{\sqrt 3 }}} \right)^3} + \dfrac{1}{{\sqrt 3 }} + c\) \( \Leftrightarrow \dfrac{{2\sqrt 3 }}{9} = \dfrac{{2\sqrt 3 }}{9} + c \Leftrightarrow c = 0\).
\( \Rightarrow f\left( x \right) = {x^3} - x\).
Vì \(F\left( x \right)\) là một nguyên hàm của \(f\left( x \right)\) nên \(F'\left( x \right) = f\left( x \right)\).
Xét hàm số \(g\left( x \right) = F\left( {f\left( x \right)} \right)\) ta có \(g'\left( x \right) = F'\left( {f\left( x \right)} \right).f'\left( x \right) = f\left( {f\left( x \right)} \right).f'\left( x \right)\).
Cho \(g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}f\left( {f\left( x \right)} \right) = 0\\f'\left( x \right) = 0\end{array} \right.\).
Ta có \(f\left( x \right) = {x^3} - x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1\\x = - 1\end{array} \right.\), \(f'\left( x \right) = 0 \Leftrightarrow x = \pm \dfrac{1}{{\sqrt 3 }}\).
Do đó \(g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = 0\\f\left( x \right) = 1\\f\left( x \right) = - 1\\x = \pm \dfrac{1}{{\sqrt 3 }}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{x^3} - x = 0\\{x^3} - x = 1\\{x^3} - x = - 1\\x = \pm \dfrac{1}{{\sqrt 3 }}\end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}x = 0,\,\,x = - 1,\,\,x = 1\\x = {x_1} \approx 1,32\\x = - {x_1} \approx - 1,32\\x = \pm \dfrac{1}{{\sqrt 3 }}\end{array} \right.\).
Chọn \(x = - 2\) ta có \(g'\left( { - 2} \right) = f\left( {f\left( { - 2} \right)} \right).f'\left( { - 2} \right) = f\left( { - 6} \right).11 < 0\), qua các nghiệm trên \(g'\left( x \right)\) đều đổi dấu (do đây đều là các nghiệm đơn).
Bảng xét dấu:
Dựa vào bảng xét dấu và các đáp án ta suy ra hàm số \(g\left( x \right) = F\left( {f\left( x \right)} \right)\) nghịch biến trên \(\left( { - \infty ; - 2} \right)\).
Chọn C.