Câu hỏi:
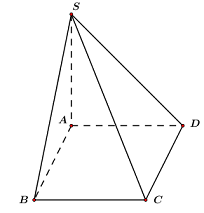
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông, \(AB = a.\) Cạnh \(SA\) vuông góc với đáy, \(SA = a\sqrt 2 .\) Khoảng cách từ trọng tâm \(G\) của \(\Delta ABC\) đến mặt phẳng \(\left( {SCD} \right)\) bằng:
- A \(\dfrac{{a\sqrt 6 }}{9}\)
- B \(\dfrac{{2a\sqrt 3 }}{{15}}\)
- C \(\dfrac{{2a}}{3}\)
- D \(\dfrac{{2a\sqrt 6 }}{9}\)
Phương pháp giải:
Gọi \(O\) là giao điểm của \(AC\) và \(BD.\)
Ta có: \(\dfrac{{GD}}{{BD}} = \dfrac{{d\left( {G;\,\left( {SCD} \right)} \right)}}{{d\left( {B;\,\,\left( {SCD} \right)} \right)}} = \dfrac{2}{3}\) \( \Rightarrow d\left( {G;\,\,\left( {SCD} \right)} \right) = \dfrac{2}{3}d\left( {B;\,\,\left( {SCD} \right)} \right)\)
Mà \(AB//CD \Rightarrow AB//\left( {SCD} \right)\) \( \Rightarrow d\left( {B;\,\,\left( {SCD} \right)} \right) = d\left( {A;\,\,\left( {SCD} \right)} \right)\)
Lời giải chi tiết:
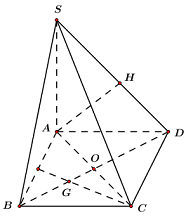
Gọi \(O\) là giao điểm của \(AC\) và \(BD.\)
Ta có: \(\dfrac{{GD}}{{BD}} = \dfrac{{d\left( {G;\,\left( {SCD} \right)} \right)}}{{d\left( {B;\,\,\left( {SCD} \right)} \right)}} = \dfrac{2}{3}\) \( \Rightarrow d\left( {G;\,\,\left( {SCD} \right)} \right) = \dfrac{2}{3}d\left( {B;\,\,\left( {SCD} \right)} \right)\)
Mà \(AB//CD \Rightarrow AB//\left( {SCD} \right)\) \( \Rightarrow d\left( {B;\,\,\left( {SCD} \right)} \right) = d\left( {A;\,\,\left( {SCD} \right)} \right)\)
Ta có: \(\left\{ \begin{array}{l}CD \bot AD\\CD \bot SA\end{array} \right. \Rightarrow CD \bot \left( {SAD} \right)\)
Trong mặt phẳng \(\left( {SAD} \right),\) dựng \(AH \bot SD\) \( \Rightarrow CD \bot AH\)
\( \Rightarrow AH \bot \left( {SCD} \right) \Rightarrow d\left( {A;\,\,\left( {SCD} \right)} \right) = AH\)
Áp dụng hệ thức lượng trong \(SAD\) vuông tại \(A\) có đường cao \(AH\) ta có:
\(AH = \dfrac{{SA.AD}}{{\sqrt {S{A^2} + A{D^2}} }} = \dfrac{{a\sqrt 2 .a}}{{\sqrt {{{\left( {a\sqrt 2 } \right)}^2} + {a^2}} }}\) \( = \dfrac{{{a^2}\sqrt 2 }}{{a\sqrt 3 }} = \dfrac{{a\sqrt 6 }}{3}\)
\(\begin{array}{l} \Rightarrow d\left( {B;\,\,\left( {SCD} \right)} \right) = \dfrac{{a\sqrt 6 }}{3}\\ \Rightarrow d\left( {G;\,\,\left( {SCD} \right)} \right) = \dfrac{2}{3}d\left( {B;\,\,\left( {SCD} \right)} \right) = \dfrac{2}{3}.\dfrac{{a\sqrt 6 }}{3} = \dfrac{{2a\sqrt 6 }}{9}.\end{array}\)
Chọn D.


















