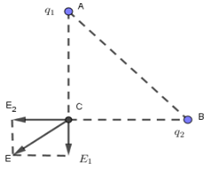
Câu hỏi:
Đặt tại hai đỉnh A và B của một tam giác vuông cân ABC (AC = BC = 90cm) lần lượt các điện tích điểm \({q_1} = 5,{4.10^{ - 6}}C\)và \(q_2.\) Cho biết hệ thống đặt trong không khí và cường độ điện trường tổng hợp tại đỉnh C có giá trị \(E = {10.10^4}V/m\). Điện tích \(q_2\) có độ lớn là
- A \({6.10^{ - 6}}C\)
- B \(4,{2.10^{ - 6}}C\)
- C \(7,{2.10^{ - 6}}C\)
- D \({8.10^{ - 6}}C\)
Phương pháp giải:
Công thức tính cường độ điện trường: \(E = k.\dfrac{{\left| q \right|}}{{{r^2}}}\)
Vẽ hình biểu điễn vecto cường độ điện trường, áp dụng định lí hàm số cos và nguyên lí chồng chất điện trường :\(\vec E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + ... + \overrightarrow {{E_n}} \)
Lời giải chi tiết:
Ta có: \(\overrightarrow {{E_C}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} \)
Vì AC vuông góc với BC \( \Rightarrow \overrightarrow {{E_1}} \bot \overrightarrow {{E_2}} \)
Giả sử \({q_2} > 0\) ta có cường độ điện trường tại C được biểu diễn như hình vẽ:
Do \(\overrightarrow {{E_1}} \bot \overrightarrow {{E_2}} \Rightarrow {E_C} = \sqrt {E_1^2 + E_2^2} \Rightarrow {E_2} = \sqrt {E_C^2 - E_1^2} \)
Mà: \(\left\{ \begin{array}{l}{E_C} = {10.10^4}V/m\\{E_1} = \dfrac{{k\left| {{q_1}} \right|}}{{A{C^2}}} = \dfrac{{{{9.10}^9}.5,{{4.10}^{ - 6}}}}{{0,{9^2}}} = {6.10^4}V/m\end{array} \right.\)
\( \Rightarrow {E_2} = \sqrt {E_C^2 - E_1^2} = {8.10^4}V/m\)
Lại có: \({E_2} = \dfrac{{k.\left| {{q_2}} \right|}}{{B{C^2}}} \Rightarrow \left| {{q_2}} \right| = \dfrac{{{E_2}.B{C^2}}}{k} = \dfrac{{{{8.10}^4}.0,{9^2}}}{{{{9.10}^9}}} = 7,{2.10^{ - 6}}C\)
Chọn C.