Phương pháp giải:

- Tính đạo hàm của hàm số.

- Chia các trường hợp của $m$, xác định nghiệm của phương trình $f'\left( x \right) = 0$.

- Lập BBT của hàm số, tìm điều kiện để $f'\left( x \right) > 0\,\,\forall x \in \left( {2; + \infty } \right)$.

Lời giải chi tiết:

Ta có $f'\left( x \right) = 4{x^3} - 4\left( {{m^2} - 3m} \right)x$.

$\begin{array}{l}f'\left( x \right) = 0 \Leftrightarrow 4x\left[ {{x^2} - \left( {{m^2} - 3m} \right)} \right] = 0\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow \left[ \begin{array}{l}x = 0\\{x^2} = {m^2} - 3m\end{array} \right.\end{array}$

TH1: ${m^2} - 3m \le 0 \Leftrightarrow 0 \le m \le 3$, khi đó ta có $f'\left( x \right) > 0\,\,\forall x > 0$, do đó hàm số đồng biến trên $\left( {0; + \infty } \right)$, thỏa mãn điều kiện hàm số đồng biến trên khoảng $\left( {2; + \infty } \right).$

TH2: ${m^2} - 3m > 0 \Leftrightarrow \left[ \begin{array}{l}m > 3\\m < 0\end{array} \right.\,\,\left( * \right)$, khi đó ta có $f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \sqrt {{m^2} - 3m}  = {x_1}\\x =  - \sqrt {{m^2} - 3m}  = {x_2}\end{array} \right.$.

Ta có BBT:

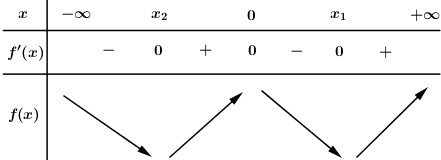
Dựa vào BBT ta thấy: Để hàm số đồng biến trên khoảng $\left( {2; + \infty } \right)$ thì ${x_1} \le 2$.

$\Leftrightarrow \sqrt {{m^2} - 3m}  \le 2 \Leftrightarrow {m^2} - 3m \le 4 \Leftrightarrow  - 1 \le m \le 4$.

Kết hợp điều kiện (*) $\Rightarrow m \in \left[ { - 1;0} \right) \cup \left( {3;4} \right]$.

Kết hợp 2 trường hợp $\Rightarrow m \in \left[ { - 1;4} \right]$.  Mà $m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 1;0;1;2;3;4} \right\}$.

Vậy có 6 giá trị của $m$ thỏa mãn yêu cầu bài toán.

Chọn B.