Phương pháp giải:

Lời giải chi tiết:

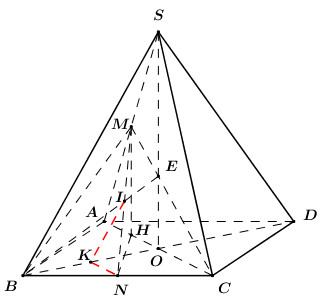
Gọi \(H\) là trung điểm của \(OA\) ta có \(MH\parallel SO \Rightarrow MH \bot \left( {ABCD} \right)\).

\( \Rightarrow HN\) là hình chiếu của \(MN\) lên \(\left( {ABCD} \right)\).

\( \Rightarrow \angle \left( {MN;\left( {ABCD} \right)} \right) = \angle \left( {MN;HN} \right) = \angle MNH = {60^0}\).

Xét tam giác \(CHN\) có: \(CN = \dfrac{1}{2}BC = \dfrac{a}{2}\), \(CH = \dfrac{3}{4}AC = \dfrac{{3a\sqrt 2 }}{4}\), \(\angle HCN = {45^0}\).

\(\begin{array}{l} \Rightarrow H{N^2} = C{H^2} + C{N^2} - 2CH.CN.\cos {45^0}\\\,\,\,\,\,\,\,H{N^2} = \dfrac{{9{a^2}}}{8} + \dfrac{{{a^2}}}{4} - 2.\dfrac{{3a\sqrt 2 }}{4}.\dfrac{a}{2}.\dfrac{{\sqrt 2 }}{2}\\\,\,\,\,\,\,\,H{N^2} = \dfrac{{5{a^2}}}{8} \Rightarrow HN = \dfrac{{a\sqrt {10} }}{4}\end{array}\)

Xét tam giác vuông \(MNH\) có: \(MN = \dfrac{{NH}}{{\cos {{60}^0}}} = \dfrac{{a\sqrt {10} }}{2}\).

Trong \(\left( {SAC} \right)\) gọi \(E = CM \cap SO\) \( \Rightarrow \left( {MBC} \right) \cap \left( {SBD} \right) = BE\).

Trong \(\left( {MBC} \right)\) gọi \(I = MN \cap BE \Rightarrow I = MN \cap \left( {SBD} \right)\).

Gọi \(K\) là trung điểm của \(OB\) \( \Rightarrow NK\parallel OC\).

Ta có: \(\left\{ \begin{array}{l}OC \bot BD\\OC \bot SO\end{array} \right. \Rightarrow OC \bot \left( {SBD} \right) \Rightarrow NK \bot \left( {SBD} \right)\).

\( \Rightarrow IK\) là hình chiếu của \(IN\) lên \(\left( {SBD} \right)\).

\( \Rightarrow \angle \left( {MN;\left( {SBD} \right)} \right) = \angle \left( {IN;\left( {SBD} \right)} \right) = \angle \left( {IN;IK} \right) = \angle NIK\).

Ta có \(NK = \dfrac{1}{2}OC = \dfrac{{a\sqrt 2 }}{4}\).

Áp dụng định lí Menelaus trong tam giác \(MAC\) ta có: \(\dfrac{{EM}}{{EC}}.\dfrac{{OC}}{{OA}}.\dfrac{{SA}}{{SM}} = 1\) \( \Leftrightarrow \dfrac{{EM}}{{EC}}.1.2 = 1 \Leftrightarrow \dfrac{{EM}}{{EC}} = \dfrac{1}{2}\).  

Áp dụng định lí Menelaus trong tam giác \(MNC\) ta có: \(\dfrac{{IM}}{{IN}}.\dfrac{{BN}}{{BC}}.\dfrac{{EC}}{{EM}} = 1 \Leftrightarrow \dfrac{{IM}}{{IN}}.\dfrac{1}{2}.2 = 1 \Leftrightarrow IM = IN\).

\( \Rightarrow IN = \dfrac{1}{2}MN = \dfrac{{a\sqrt {10} }}{4}\).

Xét tam giác vuông \(INK\) có: \(sin\angle NIK = \dfrac{{NK}}{{IN}} = \dfrac{{a\sqrt 2 }}{4}:\dfrac{{a\sqrt {10} }}{4} = \dfrac{1}{{\sqrt 5 }}\).

Vậy \(\cos \angle NIK = \sqrt {1 - {{\sin }^2}\angle NIK}  = \sqrt {1 - \dfrac{1}{5}}  = \dfrac{{2\sqrt 5 }}{5}\).

Chọn C.