Phương pháp giải:

- \(AB\parallel CD \Rightarrow AB\parallel \left( {SCD} \right)\) \( \Rightarrow d\left( {AB;\left( {SCD} \right)} \right) = d\left( {A;\left( {SCD} \right)} \right)\).

- Trong \(\left( {ABCD} \right)\) kẻ \(AE \bot CD\) (\(E\) thuộc phần kéo dài của \(CD\)), trong \(\left( {SAE} \right)\) kẻ \(AH \bot SE\,\,\left( {H \in SE} \right)\). Chứng minh \(AH \bot \left( {SCD} \right)\).

- Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông và hệ thức lượng trong tam giác vuông để tính khoảng cách.

Lời giải chi tiết:

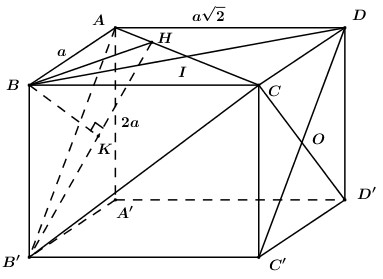
+ \(OD\parallel AB' \Rightarrow OD\parallel \left( {AB'C} \right)\) \( \Rightarrow d\left( {O;\left( {AB'C} \right)} \right) = d\left( {D;\left( {AB'C} \right)} \right)\).

+ Gọi \(I = AC \cap BD\) \( \Rightarrow I\) là trung điểm của \(AC,\,\,BD\).

+ \(DB \cap \left( {AB'C} \right) = I \Rightarrow \dfrac{{d\left( {D;\left( {AB'C} \right)} \right)}}{{d\left( {B;\left( {AB'C} \right)} \right)}} = \dfrac{{DI}}{{BI}} = 1\) \( \Rightarrow d\left( {D;\left( {AB'C} \right)} \right) = d\left( {B;\left( {AB'C} \right)} \right)\).

Trong \(\left( {ABCD} \right)\) dựng \(BH \bot AC\,\,\left( {H \in AC} \right)\), trong \(\left( {BB'H} \right)\) dựng \(BK \bot B'H\,\,\left( {K \in B'I} \right)\).

+ \(\left\{ \begin{array}{l}AC \bot BH\\AC \bot BB'\end{array} \right. \Rightarrow AC \bot \left( {BB'H} \right) \Rightarrow AC \bot BK\).

+ \(\left\{ \begin{array}{l}BK \bot AC\\BK \bot B'H\end{array} \right. \Rightarrow BK \bot \left( {AB'C} \right)\) \( \Rightarrow d\left( {B;\left( {AB'C} \right)} \right) = BK\).

+ \(\Delta ABC:\,\,BH = \dfrac{{AB.BC}}{{\sqrt {A{B^2} + A{C^2}} }} = \dfrac{{a.a\sqrt 2 }}{{\sqrt {{a^2} + 2{a^2}} }} = \dfrac{{a\sqrt 6 }}{3}\).

+ \(\Delta BB'H:\,\,BK = \dfrac{{BB'.BH}}{{\sqrt {BB{'^2} + B{H^2}} }} = \dfrac{{2a.\dfrac{{a\sqrt 6 }}{3}}}{{\sqrt {4{a^2} + \dfrac{{2{a^2}}}{3}} }} = \dfrac{{2a\sqrt 7 }}{7}\).

Vậy \(d\left( {O;\left( {AB'C} \right)} \right) = \dfrac{{2a\sqrt 7 }}{7}\).