Phương pháp giải:

- Xác định quỹ tích các điểm biểu diễn số phức \(z\).

- Gọi \(M\) là điểm biểu diễn số phức \(z\), \(N\left( { - 2;1} \right)\) là điểm biểu diễn số phức \( - 2 + i\), khi đó ta có \(\left| {z + 2 - i} \right| = MN\).

- Dựa vào hình vẽ xác định vị trí của điểm \(M\) để \(M{N_{\max }}\).

Lời giải chi tiết:

Vì \(z\) thỏa mãn \(\left| {z + 1 - 2i} \right| = 2\) nên tập hợp các điểm biểu diễn số phức \(z\) là đường tròn tâm \(I\left( { - 1;2} \right)\), bán kính \(R = 2\).

Gọi \(M\) là điểm biểu diễn số phức \(z\), \(N\left( { - 2;1} \right)\) là điểm biểu diễn số phức \( - 2 + i\), khi đó ta có \(\left| {z + 2 - i} \right| = MN\).

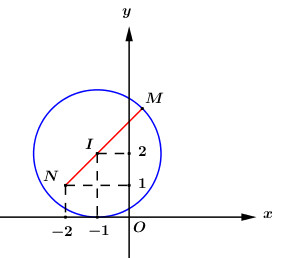
Khi đó ta có \(MN\) đạt giá trị lớn nhất khi và chỉ khi \(MN = IN + R = 2 + \sqrt 2 \).

Chọn D.