Phương pháp giải:

Gọi số phức \(z = x - yi\,\,\,\left( {x,\,\,y \in \mathbb{R}} \right)\)

Biến đổi biểu thức \(\left| {z - i} \right| \le 1\) để tìm quỹ tích của số phức bài cho.

Lời giải chi tiết:

Gọi số phức \(z = x - yi\,\,\,\left( {x,\,\,y \in \mathbb{R}} \right)\)

Ta có: \(\left| {z - i} \right| \le 1\)

\(\begin{array}{l} \Leftrightarrow \left| {x + yi - i} \right| \le 1\\ \Leftrightarrow \left| {x + \left( {y - 1} \right)i} \right| \le 1\\ \Leftrightarrow {x^2} + {\left( {y - 1} \right)^2} \le 1\end{array}\)

\( \Rightarrow \) Quỹ tích của số phức \(z\) thỏa mãn bài cho là hình tròn tâm \(I\left( {0;\,\,1} \right),\) bán kính \(R = 1.\)

Chọn D. 

Phương pháp giải:

- Sử dụng phương pháp lấy môđun hai vế.

- Áp dụng công thức \(\left| {{z^2}} \right| = {\left| z \right|^2}\).

Lời giải chi tiết:

Gọi số phức \(z = a + bi\,\,\left( {a,\,\,b \in \mathbb{R}} \right)\), theo bài ra ta có:

\(\begin{array}{l}{a^2} - {b^2} + 2abi = {a^2} + {b^2}\\ \Leftrightarrow 2{b^2} = 2abi\\ \Leftrightarrow 2b\left( {b - ai} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}2b = 0\\b - ai = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}b = 0\\a = b = 0\end{array} \right.\end{array}\)

Vậy tập hợp các số phức thỏa mãn yêu câu bài toán là các số phức có phần ảo bằng \(0\) và số \(0\), chính là tập \(\mathbb{R}\).

Chọn A.

Phương pháp giải:

- Đặt \(z = a + bi\). Áp dụng công thức tính môđun số phức: \(z = a + bi \Rightarrow \left| z \right| = \sqrt {{a^2} + {b^2}} \).

- Biến đổi rút ra mối quan hệ giữa \(a,\,\,b\) và suy ra quỹ tích các điểm biểu diễn số phức \(z\).

Lời giải chi tiết:

Đặt \(z = a + bi\,\,\left( {a,\,\,b \in \mathbb{R}} \right).\)

Theo bài ra ta có:

\(\begin{array}{l}\,\,\,\,\,\,\,\left| {z + 1 + 3i} \right| = \left| {z - 2 - i} \right|\\ \Leftrightarrow \left| {a + bi + 1 + 3i} \right| = \left| {a + bi - 2 - i} \right|\\ \Leftrightarrow {\left( {a + 1} \right)^2} + {\left( {b + 3} \right)^2} = {\left( {a - 2} \right)^2} + {\left( {b - 1} \right)^2}\\ \Leftrightarrow {a^2} + 2a + 1 + {b^2} + 6b + 9 = {a^2} - 4a + 4 + {b^2} - 2b + 1\\ \Leftrightarrow 6a + 8b + 5 = 0\end{array}\)

Suy ra tập hợp các điểm \(M\) biểu diễn số phức \(z\) là đường thẳng \(6x + 8y + 5 = 0\).

Dựa vào các đáp án ta có: Với \(A\left( { - 1; - 3} \right),\,\,B\left( {2;1} \right)\) \( \Rightarrow \) trung điểm của đoạn \(AB\)  là \(I\left( {\dfrac{1}{2}; - 1} \right)\).

\(\overrightarrow {AB}  = \left( {3;4} \right)\) là 1 VTPT của đường trung trực của AB.

Suy ra phương trình đường trung trực của AB là:

\(3\left( {x - \dfrac{1}{2}} \right) + 4\left( {y + 1} \right) = 0 \Leftrightarrow 3x + 4y + \dfrac{5}{2} = 0 \Leftrightarrow 6x + 8y + 5 = 0\).

Vậy tập hợp điểm biểu diễn của số phức \(z\) là đường trung trực của đoạn thẳng AB.

Chọn D.

Phương pháp giải:

- Gọi \(z = x + yi\) .

- Thay vào giả thiết, biến đổi và suy ra phương trình biểu diễn mối quan hệ giữa \(x\) và \(y\).

- Sử dụng công thức tính môđun số phức: \(z = a + bi \Rightarrow \left| z \right| = \sqrt {{a^2} + {b^2}} \).

Lời giải chi tiết:

Đặt \(z = x + yi\), theo bài ra ta có:

\(\begin{array}{l}\left| {z - i} \right| = \left| {2 - 3i - z} \right|\\ \Leftrightarrow \left| {x + yi - i} \right| = \left| {2 - 3i - x - yi} \right|\\ \Leftrightarrow \left| {x + \left( {y - 1} \right)i} \right| = \left| {\left( {2 - x} \right) - \left( {3 + y} \right)i} \right|\\ \Leftrightarrow {x^2} + {\left( {y - 1} \right)^2} = {\left( {2 - x} \right)^2} + {\left( {3 + y} \right)^2}\\ \Leftrightarrow {x^2} + {y^2} - 2y + 1 = {x^2} - 4x + 4 + {y^2} + 6y + 9\\ \Leftrightarrow 4x - 8y - 12 = 0\\ \Leftrightarrow x - 2y - 3 = 0\end{array}\)

Vậy tập hợp các điểm biểu diễn số phức \(z\) thỏa mãn \(\left| {z - i} \right| = \left| {2 - 3i - z} \right|\) là đường thẳng có phương trình \(x - 2y - 3 = 0.\)

Chọn C.

Phương pháp giải:

- Giải phương trình bậc hai tìm hai số phức \({z_1},\,\,{z_2}\) .

- Đặt \(w = x + yi\,\,\left( {x,\,\,y \in \mathbb{R}} \right)\), thay vào giả thiết tìm mối quan hệ giữa \(x,\,\,y\).

- Sử dụng công thức tính môđun số phức: \(z = a + bi \Rightarrow \left| z \right| = \sqrt {{a^2} + {b^2}} \).

Lời giải chi tiết:

Ta có: \({z^2} - 2z + 2 = 0 \Leftrightarrow \left[ \begin{array}{l}{z_1} = 1 + i\\{z_2} = 1 - i\end{array} \right.\).

Theo bài ra ta có: \(\left| {w - {z_1}} \right| = \left| {w - {z_2}} \right| \Leftrightarrow \left| {w - 1 - i} \right| = \left| {w - 1 + i} \right|\).

Đặt \(w = x + yi\,\,\left( {x,\,\,y \in \mathbb{R}} \right)\) ta có:

\(\begin{array}{l}\,\,\,\,\,\,\left| {x + yi - 1 - i} \right| = \left| {x + yi - 1 + i} \right|\\ \Leftrightarrow \left| {\left( {x - 1} \right) + \left( {y - 1} \right)i} \right| = \left| {\left( {x - 1} \right) + \left( {y + 1} \right)i} \right|\\ \Leftrightarrow {\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = {\left( {x - 1} \right)^2} + {\left( {y + 1} \right)^2}\\ \Leftrightarrow {y^2} - 2y + 1 = {y^2} + 2y + 1\\ \Leftrightarrow y = 0\end{array}\) 

Vậy tập hợp các điểm biểu diễn của số phức \(w\) là đường thẳng có phương trình \(y = 0\).

Chọn D.

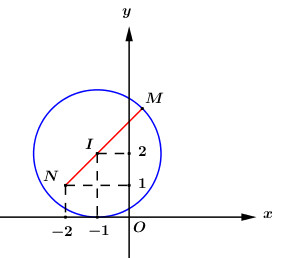
Phương pháp giải:

- Xác định quỹ tích các điểm biểu diễn số phức \(z\).

- Gọi \(M\) là điểm biểu diễn số phức \(z\), \(N\left( { - 2;1} \right)\) là điểm biểu diễn số phức \( - 2 + i\), khi đó ta có \(\left| {z + 2 - i} \right| = MN\).

- Dựa vào hình vẽ xác định vị trí của điểm \(M\) để \(M{N_{\max }}\).

Lời giải chi tiết:

Vì \(z\) thỏa mãn \(\left| {z + 1 - 2i} \right| = 2\) nên tập hợp các điểm biểu diễn số phức \(z\) là đường tròn tâm \(I\left( { - 1;2} \right)\), bán kính \(R = 2\).

Gọi \(M\) là điểm biểu diễn số phức \(z\), \(N\left( { - 2;1} \right)\) là điểm biểu diễn số phức \( - 2 + i\), khi đó ta có \(\left| {z + 2 - i} \right| = MN\).

Khi đó ta có \(MN\) đạt giá trị lớn nhất khi và chỉ khi \(MN = IN + R = 2 + \sqrt 2 \).

Chọn D.

Phương pháp giải:

Gọi số phức \(z = x + yi\,\,\left( {x,\,\,y \in \mathbb{R}} \right)\)\( \Rightarrow \overline z  = x - yi.\)

Modul của số phức \(z\) là:\(\left| z \right| = \sqrt {{x^2} + {y^2}} .\)

Điểm \(M\left( {x;\,\,y} \right)\) là điểm biểu diễn số phức \(z.\)

Lời giải chi tiết:

Gọi số phức \(z = x + yi\,\,\left( {x,\,\,y \in \mathbb{R}} \right)\)\( \Rightarrow \overline z  = x - yi.\) Ta có:

\(\begin{array}{l}\left| {z - 2} \right| = \left| {\overline z  + i} \right|\\ \Leftrightarrow \left| {x + yi - 2} \right| = \left| {x - yi + i} \right|\\ \Leftrightarrow \sqrt {{{\left( {x - 2} \right)}^2} + {y^2}}  = \sqrt {{x^2} + {{\left( {y - 1} \right)}^2}} \\ \Leftrightarrow {\left( {x - 2} \right)^2} + {y^2} = {x^2} + {\left( {y - 1} \right)^2}\\ \Leftrightarrow 4 - 4x = 1 - 2y\\ \Leftrightarrow 4x - 2y - 3 = 0\end{array}\)  

\( \Rightarrow \) Tập hợp điểm biểu diễn số phức \(z\) đã cho là đường thẳng có phương trình \(4x - 2y - 3 = 0.\)

Chọn C.

Phương pháp giải:

- Tìm điểm biểu diễn của các số phức.

- Dựa vào diện tích tam giác để xác định các số phức.

Lời giải chi tiết:

Đặt \(z = a + bi \Rightarrow {\rm{w}} = \left( {1 + i} \right)\left( {a + bi} \right) = a - b + \left( {a + b} \right)i\)

Khi đó \(A\left( {a;b} \right);B\left( {a - b;a + b} \right)\)

Số phức \(z' = {\rm{w}} - z =  - b + ai\)

Ta có \(\left| z \right| = \sqrt {{a^2} + {b^2}} ;\left| {\rm{w}} \right| = \sqrt {{{\left( {a - b} \right)}^2} + {{\left( {a + b} \right)}^2}}  = \sqrt 2 .\sqrt {{a^2} + {b^2}} \)\( \Rightarrow OA = \sqrt 2 .OB\)

Mà \(\left| {z'} \right| = AB = OA\)

Tam giác OAB có \(OA = AB;OB = \sqrt 2 OA\) nên tam giác vuông cân tại A.

\( \Rightarrow {S_{OAB}} = \dfrac{{A{B^2}}}{2} = 8 \Rightarrow AB = 4 \Rightarrow \left| {{\rm{w}} - z} \right| = 4\)

Chọn D.

Phương pháp giải:

Đặt \(z = a + bi\) rồi thay vào biểu thức đề bài để lập luận.

Lời giải chi tiết:

Đặt \(z = a + bi\)\( \Rightarrow \overline z  = a - bi\)

Khi đó \(\left( {z + 4i} \right)\left( {\overline z  + 6} \right) = \left( {a + \left( {b + 4} \right)i} \right)\left( {a + 6 - bi} \right) = a\left( {a + 6} \right) + b\left( {b + 4} \right) + \left[ {\left( {a + 6} \right)\left( {b + 4} \right) - ab} \right]i\)

Là số thuần ảo nên \(a\left( {a + 6} \right) + b\left( {b + 4} \right) = 0 \Leftrightarrow {\left( {a + 3} \right)^2} + {\left( {b + 2} \right)^2} = 13\)

Suy ra điểm biểu diễn của số phức z là đường tròn tâm \(I\left( { - 3; - 2} \right)\)

Chọn D.

Phương pháp giải:

- Tìm tập hợp các điểm biểu diễn số phức z.

- Gọi \(M\left( {a;b} \right)\) là điểm biểu diễn số phức z.

- Khi đó: \({\left| z \right|_{\min }} \Leftrightarrow O{M_{\min }}\).

Lời giải chi tiết:

Vì  \(\left| {z - 2 - 8i} \right| = \sqrt {17} \)nên tập hợp điểm biểu diễn của số phức z là đường tròn (C) tâm \(I\left( {2;8} \right)\), bán kính \(R = \sqrt {17} .\)

Gọi \(M\left( {a;b} \right)\) là điểm biểu diễn số phức z. Khi đó ta có \(\left| z \right| = OM\).

Do đó \({\left| z \right|_{\min }} \Leftrightarrow O{M_{\min }} \Rightarrow M\) là giao điểm của đường thẳng OI và đường tròn (C).

Ta có đường thẳng OI có dạng \(y = 4x\)

M là giao điểm của đường thẳng OI và đường tròn (C) nên tọa độ điểm M là nghiệm của hệ phương trình: \(\begin{array}{l}\left\{ \begin{array}{l}y = 4x\\{\left( {x - 2} \right)^2} + {\left( {y - 8} \right)^2} = 17\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 4x\\{\left( {x - 2} \right)^2} + {\left( {4x - 8} \right)^2} = 17\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}y = 4x\\17{\left( {x - 2} \right)^2} = 17\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 4x\\{\left( {x - 2} \right)^2} = 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}y = 4x\\\left[ \begin{array}{l}x - 2 = 1\\x - 2 =  - 1\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 3,\,\,y = 12\\x = 1,\,\,y = 4\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}M\left( {3;12} \right)\\M\left( {1;4} \right)\end{array} \right.\end{array}\)

Với M(3;12) thì \(OM = \sqrt {{3^2} + {{12}^2}}  = 3\sqrt {17} \).

Với M(1;4) thì \(OM = \sqrt {{1^2} + {4^2}}  = \sqrt {17} \).

Vậy \(O{M_{\min }} = \sqrt {17}  \Leftrightarrow a = 1,\,\,b = 4\) \( \Rightarrow m = 2{a^2} - 3b =  - 10.\)

Chọn C.

Phương pháp giải:

- Đặt \(z = x + yi \Rightarrow \overline z  = x - yi\).

- Thay vào biểu thức đề bài cho và suy ra biểu thức biểu diễn mối liên hệ giữa \(x,\,\,y\).

Lời giải chi tiết:

Đặt \(z = x + yi \Rightarrow \overline z  = x - yi\).

Theo bài ra ta có:

\(\begin{array}{l}\,\,\,\,\,\left| {z - 2 - i} \right| = \left| {\overline z  + 2i} \right|\\ \Leftrightarrow \left| {x + yi - 2 - i} \right| = \left| {x - yi + 2i} \right|\\ \Leftrightarrow \left| {\left( {x - 2} \right) + \left( {y - 1} \right)i} \right| = \left| {x - \left( {y - 2} \right)i} \right|\\ \Leftrightarrow {\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} = {x^2} + {\left( {y - 2} \right)^2}\\ \Leftrightarrow {x^2} - 4x + 4 + {y^2} - 2y + 1 = {x^2} + {y^2} - 4y + 4\\ \Leftrightarrow 4x - 2y - 1 = 0\end{array}\)

Vậy tập hợp các điểm biểu diễn các số phức z thảo mãn \(\left| {z - 2 - i} \right| = \left| {\overline z  + 2i} \right|\) là đường thẳng \(4x - 2y - 1 = 0\).

Chọn C.

Phương pháp giải:

- Gọi \(M\left( {2a - 1;a} \right)\) thuộc đường thẳng \(x - 2y + 1 = 0\) \( \Rightarrow \) Số phức \({z_3}\).

- Tính \(w\) và tính \(\left| w \right|\).

- Đưa biểu thức về dạng bình phương và tìm GTNN.

Lời giải chi tiết:

Gọi \(M\left( {2a - 1;a} \right)\) thuộc đường thẳng \(x - 2y + 1 = 0\) \( \Rightarrow {z_3} = 2a - 1 + ai\).

Khi đó ta có:

\(\begin{array}{l}w = 3{z_3} - {z_2} - 2{z_1}\\w = 3\left( {2a - 1 + ai} \right) - \left( { - 5 - 3i} \right) - 2\left( {1 + 3i} \right)\\w = \left( {6a - 3 + 5 - 2} \right) + \left( {3a + 3 - 6} \right)i\\w = 6a + \left( {3a - 3} \right)i\end{array}\)

\(\begin{array}{l} \Rightarrow \left| w \right| = \sqrt {{{\left( {6a} \right)}^2} + {{\left( {3a - 3} \right)}^2}} \\\,\,\,\,\,\,\left| w \right| = \sqrt {45{a^2} - 18a + 9} \\\,\,\,\,\,\,\left| w \right| = \sqrt {45\left( {{a^2} - \dfrac{2}{5}a} \right) + 9} \\\,\,\,\,\,\,\left| w \right| = \sqrt {45\left( {{a^2} - 2.a.\dfrac{1}{5} + \dfrac{1}{{25}}} \right) - \dfrac{9}{5} + 9} \\\,\,\,\,\,\,\left| w \right| = \sqrt {45{{\left( {a - \dfrac{1}{5}} \right)}^2} + \dfrac{{36}}{5}} \\ \Rightarrow \left| w \right| \ge \sqrt {\dfrac{{36}}{5}}  = \dfrac{6}{{\sqrt 5 }}\\ \Rightarrow {\left| w \right|_{\min }} = \dfrac{6}{{\sqrt 5 }} \Leftrightarrow a = \dfrac{1}{5}\end{array}\)

Vậy \({\left| w \right|_{\min }} \Leftrightarrow M\left( { - \dfrac{3}{5};\dfrac{1}{5}} \right)\).

Chọn A.

Phương pháp giải:

- Đặt \(z = x + yi \Rightarrow \overline z  = x - yi\).

- Thay vào giả thiết, tìm quỹ tích các điểm biểu diễn số phức \(z\) là 1 đường thẳng \(d\).

- Khi đó \(\left| z \right|\) nhỏ nhất \( \Leftrightarrow \left| z \right| = d\left( {O;d} \right)\).

- Khoảng cách từ \(M\left( {{x_0};{y_0}} \right)\) đến đường thẳng \(d:\,\,ax + by + c = 0\) là \(d\left( {M;d} \right) = \dfrac{{\left| {a{x_0} + b{y_0} + c{z_0}} \right|}}{{\sqrt {{a^2} + {b^2}} }}\).

Lời giải chi tiết:

Đặt \(z = x + yi \Rightarrow \overline z  = x - yi\)

Khi đó

\(\begin{array}{l}\,\,\,\,\,\left| {z + i - 1} \right| = \left| {\overline z  - 2i} \right|\\ \Leftrightarrow \left| {x + yi + i - 1} \right| = \left| {x - yi - 2i} \right|\\ \Leftrightarrow \left| {\left( {x - 1} \right) + \left( {y + 1} \right)i} \right| = \left| {x - \left( {y + 2} \right)i} \right|\\ \Leftrightarrow {\left( {x - 1} \right)^2} + {\left( {y + 1} \right)^2} = {x^2} + {\left( {y + 2} \right)^2}\\ \Leftrightarrow {x^2} - 2x + 1 + {y^2} + 2y + 1 = {x^2} + {y^2} + 4y + 4\\ \Leftrightarrow 2x + 2y + 2 = 0\\ \Leftrightarrow x + y + 1 = 0\end{array}\)

Do đó tập hợp các điểm biểu diễn số phức \(z\) là đường thẳng \(\left( d \right):\,\,x + y + 1 = 0\).

Khi đó \(\left| z \right| = OM\) đạt giá trị nhỏ nhất \( \Leftrightarrow OM = d\left( {O;d} \right) = \dfrac{{\left| {0 + 0 + 1} \right|}}{{\sqrt {{1^2} + {1^2}} }} = \dfrac{{\sqrt 2 }}{2}\).

Chọn C.

Phương pháp giải:

- Đặt \(z = x + yi \Rightarrow \overline z  = x - yi\).

- Thay \(z,\,\,\overline z \) vào phương trình đề bài cho.

- Sử dụng công thức \(\left| {a + bi} \right| = \sqrt {{a^2} + {b^2}} \).

- Bình phương hai vế, tìm mối quan hệ giữa \(x,\,\,y\) và kết luận.

Lời giải chi tiết:

Đặt \(z = x + yi \Rightarrow \overline z  = x - yi\). Theo bài ra ta có:

\(\begin{array}{l}\,\,\,\,\,\,\left| {z + i - 1} \right| = \left| {\overline z  - 2i} \right|\\ \Leftrightarrow \left| {x + yi + i - 1} \right| = \left| {x - yi - 2z} \right|\\ \Leftrightarrow \left| {x - 1 + \left( {y + 1} \right)i} \right| = \left| {x - \left( {y + 2} \right)i} \right|\\ \Leftrightarrow {\left( {x - 1} \right)^2} + {\left( {y + 1} \right)^2} = {x^2} + {\left( {y + 2} \right)^2}\\ \Leftrightarrow {x^2} - 2x + 1 + {y^2} + 2y + 1 = {x^2} + {y^2} + 4y + 4\\ \Leftrightarrow 2x + 2y + 2 = 0\\ \Leftrightarrow x + y + 1 = 0\end{array}\)

Vậy tập hợp các điểm biểu diễn số phức \(z\) là đường thẳng có phương trình \(x + y + 1 = 0\).

Chọn A.

Phương pháp giải:

- Sử dụng tính chất: \(\left| z \right| = \left| {\overline z } \right|\).

- Rút \(\overline z \) từ giả thiết, đưa phương trình về dạng \(\left| {w - \left( {a + bi} \right)} \right| = R\). Khi đó tập hợp điểm biểu diễn số phức \(w\) là một đường tròn có tâm là điểm biểu diễn số phức \(a + bi\).

Lời giải chi tiết:

Vì \(\left| z \right| = 3\) nên \(\left| {\overline z } \right| = 3\). Mà \(w = \overline z  + i \Rightarrow \overline z  = w - i\).

Khi đó ta có: \(\left| {w - i} \right| = 3\).

Vậy tập tập hợp điểm biểu diễn số phức \(w = \overline z  + i\) là một đường tròn có tâm là điểm biểu diễn số phức \(i\), chính là điểm \(\left( {0;1} \right)\).

Chọn A.

Phương pháp giải:

Gọi \(z = a + bi \Rightarrow \overline z  = a - bi\). Thay vào biểu thức đã cho rồi suy ra đường thẳng.

Lời giải chi tiết:

Đặt \(z = a + bi \Rightarrow \overline z  = a - bi\,\,\left( {a,\,\,b \in \mathbb{R}} \right)\)

Ta có \(\left| {z + 1 - 2i} \right| = \left| {\overline z  - 2 + i} \right|\).

\(\begin{array}{l} \Leftrightarrow \left| {a + 1 + \left( {b - 2} \right)i} \right| = \left| {a - 2 - \left( {b - 1} \right)i} \right|\\ \Leftrightarrow {\left( {a + 1} \right)^2} + {\left( {b - 2} \right)^2} = {\left( {a - 2} \right)^2} + {\left( {b - 1} \right)^2}\\ \Leftrightarrow {a^2} + 2a + 1 + {b^2} - 4b + 4 = {a^2} - 4a + 4 + {b^2} - 2b + 1\\ \Leftrightarrow 6a - 2b = 0 \Leftrightarrow 3a - b = 0\end{array}\)

Vậy tập hợp các điểm biểu diễn số phức \(z\) là đường thẳng \(3x - y = 0\).

Chọn A.

Phương pháp giải:

- Tìm tọa độ điểm \(M\).

- Tìm quỹ tích điểm \(N\) là một đường thẳng \(d\), xác định phương trình đường thẳng.

- Khi đó \(M{N_{\min }} \Leftrightarrow MN = d\left( {M;d} \right)\).

- Khoảng cách từ \(M\left( {{x_0};{y_0}} \right)\) đến đường thẳng \(d:\,\,ax + by + c = 0\) là \(d\left( {M;d} \right) = \dfrac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\).

Lời giải chi tiết:

Ta có \(M\) là điểm biểu diễn số phức \({z_1} = a + \left( {{a^2} - 2a + 2} \right)i\)  \( \Rightarrow M\left( {a;{a^2} - 2a + 2} \right)\).

Gọi \(N\left( {x;y} \right)\) là điểm biểu diễn của số phức \({z_2}\) \( \Rightarrow {z_2} = x + yi.\)

\(\begin{array}{l}\left| {x + yi - 2 - i} \right| = \left| {x + yi - 6 + i} \right|\\ \Leftrightarrow {\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} = {\left( {x - 6} \right)^2} + {\left( {y + 1} \right)^2}\\ \Leftrightarrow {x^2} - 4x + 4 + {y^2} - 2y + 1 = {x^2} - 12x + 36 + {y^2} + 2y + 1\\ \Leftrightarrow 8x - 4y - 32 = 0\\ \Leftrightarrow 2x - y - 8 = 0\end{array}\)

\( \Rightarrow \) Tập hợp các điểm biểu diễn số phức \({z_2}\) là đường thẳng \(d:\,\,2x - y - 8 = 0\).

Khi đó \(M{N_{\min }} = d\left( {M;\left( d \right)} \right) = \dfrac{{\left| {2a - \left( {{a^2} - 2a + 2} \right) - 8} \right|}}{{\sqrt 5 }} = \dfrac{{\left| {{{\left( {a - 2} \right)}^2} + 6} \right|}}{{\sqrt 5 }} \ge \dfrac{{6\sqrt 5 }}{5}.\)

Chọn A.

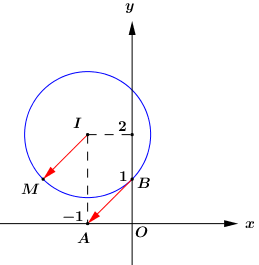
Phương pháp giải:

- Sử dụng phương pháp hình học xác định tập hợp các điểm biểu diễn số phức \(z\).

- Tập hợp các điểm biểu diễn số phức \(z\) thỏa mãn \(\left| {z - \left( {a + bi} \right)} \right| = R\) là đường tròn tâm \(I\left( {a;b} \right)\), bán kính \(R\).

- Gọi \(M,\,\,A,\,\,B\) lần lượt là điểm biểu diễn các số phức \(z,\,\, - 1,\,\,i\). Xác định tọa độ các điểm \(M,\,\,A,\,\,B\). Đưa biểu thức \({\left| {z + 1} \right|^2} - {\left| {z - i} \right|^2}\)về biểu thức trong hình học (\(M{A^2} - M{B^2}\)).

- Xác định yếu tố cố định, yếu tố thay đổi, từ đó tìm GTLN.

Lời giải chi tiết:

Giả sử \(z = x + yi\,\,\left( {x,y \in \mathbb{R}} \right)\) và \(M\left( {x;y} \right)\) là điểm biểu diễn của số phức \(z\) trong mặt phẳng toạ độ \(Oxy\).

Ta có : \(\left| {z + 1 - 2i} \right| = \sqrt 2  \Leftrightarrow \left| {z - \left( { - 1 + 2i} \right)} \right| = \sqrt 2 .\)

\( \Rightarrow \) Tập hợp các điểm \(M\) là đường tròn tâm \(I\left( { - 1;2} \right)\), bán kính \(R = \sqrt 2 \).

Gọi \(A\left( { - 1;0} \right),\,B\left( {0;1} \right)\) lần lượt là điểm biểu diễn các số phức \({z_1} =  - 1,\,\,{z_2} = i\).

Ta có: \(T = {\left| {\left( {x + 1} \right) + yi} \right|^2} - {\left| {x + \left( {y - 1} \right)i} \right|^2} = M{A^2} - M{B^2}.\)

  \(\begin{array}{l} = {\overrightarrow {MA} ^2} - {\overrightarrow {MB} ^2} = {\left( {\overrightarrow {MI}  + \overrightarrow {IA} } \right)^2} - {\left( {\overrightarrow {MI}  + \overrightarrow {IB} } \right)^2}\\ = M{I^2} + 2.\overrightarrow {MI} .\overrightarrow {IA}  + I{A^2} - M{I^2} - 2.\overrightarrow {MI} .\overrightarrow {IB}  - I{B^2}\\ = {2^2} - {\left( {\sqrt 2 } \right)^2} + 2.\overrightarrow {MI} .\left( {\overrightarrow {IA}  - \overrightarrow {IB} } \right)\\ = 2 + 2.\overrightarrow {MI} .\overrightarrow {AB} \\ = 2 + 2.MI.AB.{\rm{cos}}\left( {\overrightarrow {MI} ;\overrightarrow {BA} } \right)\\ \le 2 + 2MI.AB\end{array}\) 

Ta có: \(M \in \left( {I;\sqrt 2 } \right) \Rightarrow MI = \sqrt 2 \), \(AB = \sqrt {{1^2} + {1^2}}  = \sqrt 2 \).

\( \Rightarrow T \le 2 + 2.\sqrt 2 .\sqrt 2  = 6\).

Vậy \({T_{{\rm{max}}}} = 6\) khi và chỉ khi \({\rm{cos}}\left( {\overrightarrow {MI} ;\overrightarrow {BA} } \right) = 1\) hay hai vectơ \(\overrightarrow {MI} ,\,\,\overrightarrow {BA} \) cùng hướng.

Chọn D.

Phương pháp giải:

- Từ giả thiết \(w = \left( {3 + 4i} \right)z + i\) rút \(z\) theo \(w\).

- Thế vào giả thiết \(\left| z \right|\; = 4\), sử dụng công thức \(\left| {\frac{{{z_1}}}{{{z_2}}}} \right| = \frac{{\left| {{z_1}} \right|}}{{\left| {{z_2}} \right|}}\).

- Tập hợp các điểm biểu diễn số phức \(w\) thỏa mãn \(\left| {w - \left( {a + bi} \right)} \right| = R\) là đường tròn tâm \(I\left( {a;b} \right)\), bám kính \(R\)

Lời giải chi tiết:

Ta có:

\(w = \left( {3 + 4i} \right)z + i \Leftrightarrow \left( {3 + 4i} \right)z = w - i\)\( \Leftrightarrow z = \frac{{w - i}}{{3 + 4i}}\).

Theo bài ra ta có:

 \(\begin{array}{l}\left| z \right|\; = 4 \Leftrightarrow \left| {\frac{{w - i}}{{3 + 4i}}} \right| = 4 \Leftrightarrow \frac{{\left| {w - i} \right|}}{{\left| {3 + 4i} \right|}} = 4\\ \Leftrightarrow \frac{{\left| {w - i} \right|}}{{\sqrt {{3^2} + {4^2}} }} = 4 \Leftrightarrow \left| {w - i} \right| = 20\end{array}\)

Vậy tập hợp các điểm biểu diễn số phức \(w\) là đường tròn tâm \(I\left( {0;1} \right)\), bán kính \(r = 20\).

Chọn C.

Phương pháp giải:

Lời giải chi tiết:

Chọn C

Phương pháp giải:

- Rút \(z\) theo \(w\) từ đẳng thức bài cho. Đặt \(w = a + bi\).

- Thay vào điểu kiện \(\left| z \right| = 2\sqrt 2 \) suy ra tập hợp điểm biểu diễn \(w\).

Lời giải chi tiết:

Ta có : \(w = \dfrac{{z + 1 - i}}{{iz + 3}} \Leftrightarrow z + 1 - i = wiz + 3w \Leftrightarrow z\left( {1 - iw} \right) = 3w + i - 1 \Leftrightarrow z = \dfrac{{3w + i - 1}}{{1 - iw}}\) 

Đặt \(w = a + bi\left( {a,b \in \mathbb{R}} \right)\) thì \(z = \dfrac{{3\left( {a + bi} \right) + i - 1}}{{1 - i\left( {a + bi} \right)}} = \dfrac{{3a - 1 + \left( {3b + 1} \right)i}}{{1 + b - ai}}\)

Mà

\(\begin{array}{l}\left| z \right| = 2\sqrt 2  \Rightarrow \left| {\dfrac{{3a - 1 + \left( {3b + 1} \right)i}}{{1 + b - ai}}} \right| = 2\sqrt 2  \Leftrightarrow \dfrac{{\left| {3a - 1 + \left( {3b + 1} \right)i} \right|}}{{\left| {1 + b - ai} \right|}} = 2\sqrt 2 \\ \Leftrightarrow \sqrt {{{\left( {3a - 1} \right)}^2} + {{\left( {3b + 1} \right)}^2}}  = \sqrt {\left( {1 + {b^2}} \right) + {a^2}} .2\sqrt 2 \\ \Leftrightarrow 9{a^2} - 6a + 1 + 9{b^2} + 6b + 1 = 8\left( {{a^2} + {b^2} + 2b + 1} \right)\\ \Leftrightarrow {a^2} + {b^2} - 6a - 10b - 6 = 0 \Leftrightarrow {\left( {a - 3} \right)^2} + {\left( {b - 5} \right)^2} = 40\end{array}\)

Suy ra tập hợp điểm biểu diễn số phức \(w\) là đường tròn tâm \(I\left( {3;5} \right)\) bán kính \(R = 2\sqrt {10} \).

Chọn A.

Phương pháp giải:

Đặt \(z = a + bi\,\,\left( {a;b \in \mathbb{R}} \right) \Rightarrow \overline z  = a - bi\).

Lời giải chi tiết:

Đặt \(z = a + bi\,\,\left( {a;b \in \mathbb{R}} \right) \Rightarrow \overline z  = a - bi\).

Theo bài ra ta có:

\(\begin{array}{l}\left( {z + 1 - i} \right)\left( {\overline z  - i} \right) = \left( {a + bi + 1 - i} \right)\left( {a - bi - i} \right)\\ = \left[ {\left( {a + 1} \right) + \left( {b - 1} \right)i} \right]\left[ {a - \left( {b + 1} \right)i} \right]\\ = a\left( {a + 1} \right) + \left( {{b^2} - 1} \right) + \left[ {a\left( {b - 1} \right) - \left( {a + 1} \right)\left( {b + 1} \right)} \right]i\end{array}\)

là số thực \( \Rightarrow a\left( {b - 1} \right) - \left( {a + 1} \right)\left( {b + 1} \right) = 0 \Leftrightarrow ab - a - ab - a - b - 1 = 0 \Leftrightarrow 2a + b + 1 = 0\).

Vậy tập hợp các điểm biểu diễn hình học của \(z\) là đường thẳng \(2x + y + 1 = 0 \Leftrightarrow y =  -2 x - 1\) có hệ số góc \(k =  - 2\).

Chọn C.

Phương pháp giải:

+) Tìm tập hợp điểm biểu diễn số phức \(z\)

+) Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành và đường thẳng \(x = a;\,\,x = b\) là \(\int\limits_a^b {\left| {f\left( x \right)} \right|dx} \).

Lời giải chi tiết:

Ta có \(z = \left( {m + 3} \right) + \left( {{m^2} - m - 6} \right)i\) được biểu diễn bởi điểm \(M\left( {x;y} \right)\) với \(\left\{ \begin{array}{l}x = m + 3\\y = {m^2} - m - 6\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}m = x - 3\\y = {\left( {x - 3} \right)^2} - \left( {x - 3} \right) - 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = x - 3\\y = {x^2} - 7x + 6\end{array} \right.\).

Vậy tập hợp điểm biểu diễn số phức \(z\) là parabol \(\left( P \right):y = {x^2} - 7x + 6\)

Hoành độ giao điểm của parabol \(\left( P \right)\) với trục hoành là \({x^2} - 7x + 6 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 6\end{array} \right.\)

Diện tích hình phẳng giới hạn bởi \(\left( P \right)\) và trục hoành bằng

\(S = \int\limits_1^6 {\left| {{x^2} - 7x + 6} \right|dx}  = \left| {\int\limits_1^6 {\left( {{x^2} - 7x + 6} \right)dx} } \right| = \dfrac{{125}}{6}\)

Chọn A.

Phương pháp giải:

Lời giải chi tiết:

Chọn A.

Phương pháp giải:

Lời giải chi tiết:

Chọn C.

Phương pháp giải:

Lời giải chi tiết:

Chọn A.

Phương pháp giải:

Lời giải chi tiết:

Chọn C.

Phương pháp giải:

Lời giải chi tiết:

Chọn B.

Phương pháp giải:

+) Cô lập \(z\), thay vào điều kiện \(\left| z \right| = \sqrt 2 \).

+) Đặt \(w = x + yi\), tìm mối liên hệ giữa \(x;\,\,y\) và kết luận.

Lời giải chi tiết:

Ta có \(w = \dfrac{{5 + iz}}{{1 + z}} \Leftrightarrow w\left( {1 + z} \right) = 5 + iz \Leftrightarrow w + wz = 5 + iz \Leftrightarrow z\left( {w - i} \right) = 5 - w\).

Nếu \(w = i \Leftrightarrow 0.z = 5 - i \Leftrightarrow 0 = 5 - i\) (vô lý) \( \Rightarrow w \ne i\)\( \Rightarrow z = \dfrac{{5 - w}}{{w - i}}\).

Theo bài ra ta có:

\(\left| z \right| = \sqrt 2  \Leftrightarrow \left| {\dfrac{{5 - w}}{{w - i}}} \right| = \sqrt 2  \Leftrightarrow \left| {5 - w} \right| = \sqrt 2 \left| {w - i} \right|\).

Đặt \(w = x + yi\) ta có: \(\left| {5 - x - yi} \right| = \sqrt 2 \left| {x + yi - i} \right|\).

\(\begin{array}{l} \Leftrightarrow {\left( {5 - x} \right)^2} + {y^2} = 2\left[ {{x^2} + {{\left( {y - 1} \right)}^2}} \right]\\ \Leftrightarrow {x^2} - 10x + 25 + {y^2} = 2{x^2} + 2{y^2} - 4y + 2\\ \Leftrightarrow {x^2} + {y^2} + 10x - 4y - 23 = 0\end{array}\)  

Ta có \({a^2} + {b^2} - c = {5^2} + {2^2} + 23 = 52 > 0 \Rightarrow \) Tập hợp các điểm biểu diễn số phức \(w\) là một đường tròn có bán kính \(R = \sqrt {{a^2} + {b^2} - c}  = \sqrt {52}  = 2\sqrt {13} \).

Chọn B

Phương pháp giải:

Rút \(z\) theo \(w\) rồi lấy mô đun hai vế, từ đó suy ra tập hợp điểm biểu diễn \(w\).

Lời giải chi tiết:

Ta có: \(w = \dfrac{{2 + iz}}{{1 + z}} \Leftrightarrow 2 + iz = w\left( {1 + z} \right) \Leftrightarrow 2 - w = \left( {w - i} \right)z \Leftrightarrow z = \dfrac{{2 - w}}{{w - i}}\)

Mà \(\left| z \right| = \sqrt 2  \Rightarrow \left| {\dfrac{{2 - w}}{{w - i}}} \right| = \sqrt 2  \Leftrightarrow \left| {2 - w} \right| = \sqrt 2 \left| {w - i} \right|\).

Đặt \(w = a + bi\left( {a,b \in \mathbb{R}} \right)\) thì \(\left| {2 - w} \right| = \sqrt 2 \left| {w - i} \right| \Leftrightarrow \left| {2 - \left( {a + bi} \right)} \right| = \sqrt 2 \left| {a + bi - i} \right|\)

\( \Leftrightarrow \left| {2 - a - bi} \right| = \sqrt 2 \left| {a + \left( {b - 1} \right)i} \right|\) \( \Leftrightarrow \sqrt {{{\left( {2 - a} \right)}^2} + {b^2}}  = \sqrt 2 .\sqrt {{a^2} + {{\left( {b - 1} \right)}^2}} \)

\( \Leftrightarrow {a^2} - 4a + 4 + {b^2} = 2\left( {{a^2} + {b^2} - 2b + 1} \right)\) \( \Leftrightarrow {a^2} + {b^2} + 4a - 4b - 2 = 0 \Leftrightarrow {\left( {a + 2} \right)^2} + {\left( {b - 2} \right)^2} = 10\).

Do đó tập hợp các điểm biểu diễn \(w\) là đường tròn tâm \(\left( { - 2;2} \right)\) bán kính \(\sqrt {10} \).

Chọn D.

Phương pháp giải:

Gọi \(z = x + yi\left( {x;y \in R} \right)\). Khi đó \(\overline z  = x - yi;\left| z \right| = \sqrt {{x^2} + {y^2}} \)

Lời giải chi tiết:

Gọi \(z = x + yi\left( {x;y \in R} \right)\)

Ta có:

\(\begin{array}{l}\left| {2z - i} \right| = 2\left| {\overline z  + 1 + i} \right|\\ \Leftrightarrow \left| {2\left( {x + yi} \right) - i} \right| = 2\left| {x - yi + 1 + i} \right|\\ \Leftrightarrow \left| {2x + \left( {2y - 1} \right)i} \right| = 2\left| {\left( {x + 1} \right) + \left( {1 - y} \right)i} \right|\\ \Rightarrow 4{x^2} + {\left( {2y - 1} \right)^2} = 4{\left( {x + 1} \right)^2} + 4{\left( {1 - y} \right)^2}\\ \Leftrightarrow  - 4y + 1 = 8x + 4 - 8y + 4\\ \Leftrightarrow 8x - 4y + 7 = 0\end{array}\)

Vậy tập hợp điểm cần tìm là đường thẳng: \(8x - 4y + 7 = 0\)

Chọn C.

Phương pháp giải:

Cho số phức \(z = x + yi\;\;\left( {x,\;y \in \mathbb{R}} \right) \Rightarrow M\left( {x;\;y} \right)\) là điểm biểu diễn số phức \(z.\)

Lời giải chi tiết:

Gọi số phức \(z = x + yi\,\,\,\left( {x,\,\,y \in \mathbb{R}} \right).\)

\(\begin{array}{l} \Rightarrow \dfrac{z}{{z - 1}} = \dfrac{{x + yi}}{{x + yi - 1}} = \dfrac{{x + yi}}{{\left( {x - 1} \right) + yi}}\\ = \dfrac{{\left( {x + yi} \right)\left[ {\left( {x - 1} \right) - yi} \right]}}{{{{\left( {x - 1} \right)}^2} - {{\left( {yi} \right)}^2}}} = \dfrac{{x\left( {x - 1} \right) + {y^2} + \left( { - xy + xy - y} \right)i}}{{{{\left( {x - 1} \right)}^2} + {y^2}}}\\ = \dfrac{{{x^2} - x + {y^2}}}{{{{\left( {x - 1} \right)}^2} + {y^2}}} - \dfrac{{yi}}{{{{\left( {x - 1} \right)}^2} + {y^2}}}.\end{array}\)

Theo đề bài ta có: \(\dfrac{z}{{z - 1}}\) là số thuần ảo

\( \Rightarrow \left\{ \begin{array}{l}{x^2} - x + {y^2} = 0\\{\left( {x - 1} \right)^2} + {y^2} \ne 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}{x^2} - 2x.\dfrac{1}{2} + \dfrac{1}{4} + {y^2} - \dfrac{1}{4} = 0\\x - 1 \ne 0\\y \ne 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}{\left( {x - \dfrac{1}{2}} \right)^2} + {y^2} = \dfrac{1}{4}\\x \ne 1\\y \ne 0\end{array} \right.\)     

Vậy tập hợp các điểm biểu diễn số phức \(z\) thỏa mãn yêu cầy bài toán là đường tròn tâm \(I\left( {\dfrac{1}{2};\,\,0} \right)\) bán kính \(\dfrac{1}{2}\) trừ điểm \(A\left( {1;\,\,0} \right).\)                   

Chọn D.

Phương pháp giải:

Xác định quỹ tích các điểm biểu diễn số phức \({z_1},\,\,{z_2}\) sau đó tìm GTNN của \(\left| {{z_1} - {z_2}} \right|\).

Lời giải chi tiết:

Gọi \({z_1} = {a_1} + {b_1}i\) ta có:

\(\begin{array}{l}\,\,\,\,\,\,\left| {{a_1} + {b_1}i - 1 + i} \right| = \left| {{a_1} + {b_1}i + 3 - i} \right|\\ \Leftrightarrow {\left( {{a_1} - 1} \right)^2} + {\left( {{b_1} + 1} \right)^2} = {\left( {{a_1} + 3} \right)^2} + {\left( {{b_1} - 1} \right)^2}\\ \Leftrightarrow a_1^2 - 2{a_1} + 1 + b_1^2 + 2{b_1} + 1 = a_1^2 + 6{a_1} + 9 + b_1^2 - 2{b_1} + 1\\ \Leftrightarrow 8{a_1} - 4{b_1} + 8 = 0\\ \Leftrightarrow 2{a_1} - {b_1} + 2 = 0\end{array}\)

\( \Rightarrow \) Tập hợp các điểm \({z_1}\) là đường thẳng \(2x - y + 2 = 0\) \(\left( d \right)\).

\({z_2}\) thỏa mãn \(\left| {{z_2} - 1 + 2i} \right| = 1\) nên tập hợp các điểm \({z_2}\) là đường tròn \(\left( C \right)\) tâm \(I\left( {1; - 2} \right)\), bán kính \(R = 1\).

Gọi \(A,\,\,B\) lần lượt các các điểm biểu diễn \({z_1},\,\,{z_2}\), khi đó \(\left| {{z_1} - {z_2}} \right| = \left| {\overrightarrow {OA}  - \overrightarrow {OB} } \right| = AB\) với \(A \in \left( d \right)\), \(B \in \left( C \right)\).

Ta có \(d\left( {I;d} \right) = \dfrac{{\left| {2.1 - \left( { - 2} \right) + 2} \right|}}{{\sqrt {{2^2} + {{\left( { - 1} \right)}^2}} }} = \dfrac{6}{{\sqrt 5 }} > R\), do đó đường thẳng \(d\) không cắt \(\left( C \right)\).

Ta có: \(A{B_{\min }} = d\left( {I;d} \right) - R = \dfrac{6}{{\sqrt 5 }} - 1\).

Chọn A.

Phương pháp giải:

- Gọi \(z = x + yi\), thay vào giả thiết \(\left| {z + 2i} \right| = \left| {z - 4} \right|\) tìm tập hợp các điểm biểu diễn số phức \(z\).

- Xác định tọa độ các điểm \(A,\,\,B\) và \(C\).

- Sử dụng công thức tính diện tích tam giác: \({S_{\Delta ABC}} = \dfrac{1}{2}d\left( {A;BC} \right).BC\).

Lời giải chi tiết:

Gọi \(z = x + yi\) ta có:

\(\begin{array}{l}\left| {x + yi + 2i} \right| = \left| {x + yi - 4} \right|\\ \Leftrightarrow \sqrt {{x^2} + {{\left( {y + 2} \right)}^2}}  = \sqrt {{{\left( {x - 4} \right)}^2} + {y^2}} \\ \Leftrightarrow {x^2} + {\left( {y + 2} \right)^2} = {\left( {x - 4} \right)^2} + {y^2}\\ \Leftrightarrow {x^2} + {y^2} + 4y + 4 = {x^2} - 8x + 16 + {y^2}\\ \Leftrightarrow 8x + 4y - 12 = 0\\ \Leftrightarrow 2x + y - 3 = 0\end{array}\)

Suy ra tập hợp điểm biểu diễn số phức \(z\) là đường thẳng \(2x + y - 3 = 0\,\,\left( d \right)\).

Đường thẳng \(d\) cắt trục \(Ox\) tại \(A\left( {\dfrac{3}{2};0} \right)\), cắt trục \(Oy\) tại điểm \(B\left( {0;3} \right)\).

Điểm \(C\) là điểm biểu diễn số phức \(z =  - 3i\) nên \(C\left( {0; - 3} \right)\).

Ta có \(BC = \sqrt {{{\left( { - 6} \right)}^2}}  = 6\).

Do \(B,\,\,C \in Oy\) nên \(d\left( {A;BC} \right) = d\left( {A;Oy} \right) = \left| {{x_A}} \right| = \dfrac{3}{2}\).

Vậy \({S_{\Delta ABC}} = \dfrac{1}{2}d\left( {A;BC} \right).BC = \dfrac{1}{2}.\dfrac{3}{2}.6 = \dfrac{9}{2}\).

Chọn C.

Phương pháp giải:

- Rút \(\overline z \) theo \(w\).

- Sử dụng tính chất \(\left| z \right| = \left| {\overline z } \right|\).

- Thay \(\overline z \) theo \(w\) vào biểu thức, rút ra phương trình chứa ẩn \(w\)ở dạng \(\left| {w - \left( {a + bi} \right)} \right| = R\).

- Khi đó tập hợp các điểm biểu diễn số phức \(w\) là đường tròn có tâm \(I\left( {a;b} \right)\), bán kính \(R\).

Lời giải chi tiết:

Ta có: \(w = i\overline z  + 12 - i \Leftrightarrow \overline z  = \dfrac{{w - 12 + i}}{i}\).

Theo bài ra ta có: \(\left| {z - 2 + 3i} \right| = 5 \Rightarrow \left| {\overline {z - 2 + 3i} } \right| = 5\)\( \Leftrightarrow \left| {\overline z  + 2 - 3i} \right| = 5\,\,\left( * \right)\).

Thay \( \Leftrightarrow \overline z  = \dfrac{{w - 12 + i}}{i}\) vào (*) ta có:

\(\begin{array}{l} \Leftrightarrow \left| {\dfrac{{w - 12 + i}}{i} + 2 - 3i} \right| = 5\\ \Leftrightarrow \left| {\dfrac{{w - 12 + i + 2i + 3}}{i}} \right| = 5\\ \Leftrightarrow \dfrac{{\left| {w - 9 + 3i} \right|}}{{\left| i \right|}} = 5\\ \Leftrightarrow \left| {w - 9 + 3i} \right| = 5\end{array}\)

Vậy tập hợp các điểm biểu diễn số phức \(w\) là đường tròn có tâm \(I\left( {9; - 3} \right)\), bán kính \(R = 5\).

Chọn C.

Phương pháp giải:

Phương pháp tìm tập hợp điểm biểu diễn số phức:

Bước 1: Gọi số phức \(z = x + yi\) có điểm biểu diễn là \(M\left( {x;\,\,y} \right).\)

Bước 2: Thay \(z\) vào đề bài \( \Rightarrow \) phương trình:

+) Đường thẳng: \(Ax + By + C = 0.\)

+) Đường tròn: \({x^2} + {y^2} - 2ax - 2by + c = 0.\)

+) Parabol: \(y = a{x^2} + bx + c.\)

+) Elip: \(\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1.\)

Lời giải chi tiết:

Giả sử \(z = a + bi\,\,\,\left( {a,\,\,b \in \mathbb{R}} \right)\) ta có: \({z^2} = {\left( {a + bi} \right)^2} = {a^2} - {b^2} + 2abi.\)

Số phức \({z^2}\) có điểm biểu diễn nằm trên trục hoành \( \Leftrightarrow 2ab = 0 \Leftrightarrow \left[ \begin{array}{l}a = 0\\b = 0\end{array} \right..\)

Chọn  D.

Phương pháp giải:

Tập hợp các điểm biểu diễn của số phức z thỏa mãn: \(\left| {z - \left( {a + bi} \right)} \right| = R,\,\,\left( {a,b \in \mathbb{R}} \right)\) là đường tròn tâm \(I\left( {a;b} \right)\), bán kính \(R\). Thật vậy, giả sử số phức \(z = x + yi,\left( {x,y \in \mathbb{R}} \right)\), khi đó, ta có:

\(\left| {x + yi - \left( {a + bi} \right)} \right| = R \Leftrightarrow \left| {\left( {x - a} \right) + \left( {y - b} \right)i} \right| = R \Leftrightarrow {\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2}\)

Lời giải chi tiết:

Ta có: \(\left| {z + 2 - i} \right| = 3 \Leftrightarrow \left| {\overline {z + 2 - i} } \right| = 3 \Leftrightarrow \left| {\overline z  + \overline {2 - i} } \right| = 3 \Leftrightarrow \left| {\overline z  + 2 + i} \right| = 3 \Leftrightarrow \left| {\left( {\overline z  + 1} \right) + 1 + i} \right| = 3 \Leftrightarrow \left| {{\rm{w}} + 1 + i} \right| = 3\)

Tập hợp các điểm biểu diễn các số phức \({\rm{w}} = 1 + \overline z \) là:Đường tròn tâm \(I\left( { - 1; - 1} \right)\), bán kính \(R = 3\).

Chọn D.

Phương pháp giải:

Bước 1: Gọi số phức \(z = x + yi\,\,\,\,\left( {x,y \in R} \right)\) có điểm biểu diễn là \(M\left( {x;y} \right)\).

Bước 2: Thay \(z = x + yi\) vào điều kiện đã cho dẫn đến phương trình liên hệ giữa \(x,y\).

Bước 3: Kết luận:

- Phương trình đường thẳng: \(Ax + By + C = 0\)

- Phương trình đường tròn: \({x^2} + {y^2} - 2ax - 2by + c = 0\)

- Phương trình parabol: \(y = a{x^2} + bx + c\) hoặc \(x = a{y^2} + by + c\)

- Phương trình elip: \(\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1\)

Lời giải chi tiết:

Đặt \(z = x + yi{\rm{ }}\left( {x,y \in R} \right)\) ta có:

\(\begin{array}{l}{\left| z \right|^2} = {z^2} \Leftrightarrow {x^2} + {y^2} = {x^2} + 2xyi - {y^2}\\ \Leftrightarrow \left\{ \begin{array}{l}xy = 0\\{x^2} + {y^2} = {x^2} - {y^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \in \mathbb{R}\\y = 0\end{array} \right.\end{array}\)

Do đó tập điểm biểu diễn \(z\) là đường thẳng \(y = 0\).

Chọn B.

Phương pháp giải:

Số phức \(z = a + bi\,\,\,{\mkern 1mu} \left( {a,b \in \mathbb{R}} \right)\) là số thuần ảo khi và chỉ khi phần thực bằng 0.

Lời giải chi tiết:

Đặt \(z = a + bi\,\,\,{\mkern 1mu} \left( {a,b \in \mathbb{R}} \right)\)

\(\begin{array}{*{20}{l}}{ \Rightarrow \left( {z + 2i} \right)\left( {\bar z{\rm{\;}} + 2} \right) = \left[ {a + \left( {b + 2} \right)i} \right]\left( {a + 2 - bi} \right)}\\{ = a\left( {a + 2} \right) + b\left( {b + 2} \right) + \left[ {\left( {a + 2} \right)\left( {b + 2} \right) - ab} \right]i}\end{array}\)

Số \(\left( {z + 2i} \right)\left( {\bar z{\rm{\;}} + 2} \right)\) là số thuần ảo \( \Leftrightarrow \) Phần thực bằng 0.

\(\begin{array}{l} \Rightarrow a\left( {a + 2} \right) + b\left( {b + 2} \right) = 0\\ \Leftrightarrow {a^2} + 2a + {b^2} + 2b = 0\\ \Leftrightarrow {\left( {a + 1} \right)^2} + {\left( {b + 1} \right)^2} = 2\end{array}\)

Vậy đường tròn biểu diễn số phức đã cho có tâm là \(I\left( { - 1; - 1} \right)\).

Chọn D.

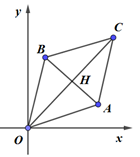
Phương pháp giải:

Sử dụng phương pháp hình học.

Lời giải chi tiết:

Giả sử A, B lần lượt là điểm biểu diễn của \({z_1},{z_2}\). Khi đó từ giả thiết \(\left| {{z_1} - {z_2}} \right| = \left| {{z_1}} \right| = \left| {{z_2}} \right| = 2\) ta suy ra \(OA = OB = AB = 2\)

\( \Leftrightarrow \Delta OAB\) đều, cạnh 2.

\( \Rightarrow \left| {{z_1} + {z_2}} \right| = OC = 2.OH = 2.\frac{{2\sqrt 3 }}{2} = 2\sqrt 3 \).

Chọn: A