Câu hỏi:
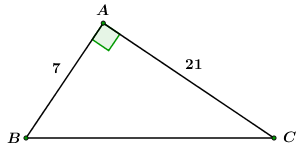
Cho tam giác \(ABC\) vuông tại \(A\). Biết \(AB{\rm{ }} = {\rm{ 7}}cm,{\rm{ }}AC{\rm{ }} = 21cm.\) Tính các tỉ số lượng giác của góc \(B\) và \(C.\)
- A \(\begin{array}{l}\sin B = \frac{3}{{\sqrt {10} }}\,\,;\,\,\cos B = \frac{1}{{\sqrt {10} }}\,\,;\,\,\tan B = 3\,\,;\,\,\,\cot B = \frac{1}{3}\\\sin C = \frac{1}{{\sqrt {10} }}\,\,;\,\,\cos C = \frac{3}{{\sqrt {10} }}\,\,;\,\,\tan C = \frac{1}{3}\,\,;\,\,\cot C = 3\end{array}\)
- B \(\begin{array}{l}\sin B = \frac{1}{{\sqrt {10} }}\,\,;\,\,\cos B = \frac{3}{{\sqrt {10} }}\,\,;\,\,\tan B = \frac{1}{3}\,\,;\,\,\,\cot B = 3\\\sin C = \frac{3}{{\sqrt {10} }}\,\,;\,\,\cos C = \frac{1}{{\sqrt {10} }}\,\,;\,\,\tan C = 3\,\,;\,\,\cot C = \frac{1}{3}\end{array}\)
- C \(\begin{array}{l}\sin B = \frac{3}{{\sqrt {10} }}\,\,;\,\,\cos B = \frac{7}{{\sqrt {10} }}\,\,;\,\,\tan B = \frac{3}{7}\,\,;\,\,\,\cot B = \frac{7}{3}\\\sin C = \frac{7}{{\sqrt {10} }}\,\,;\,\,\cos C = \frac{3}{{\sqrt {10} }}\,\,;\,\,\tan C = \frac{7}{3}\,\,;\,\,\cot C = \frac{3}{7}\end{array}\)
- D \(\begin{array}{l}\sin B = \frac{7}{{\sqrt {10} }}\,\,;\,\,\cos B = \frac{3}{{\sqrt {10} }}\,\,;\,\,\tan B = \frac{7}{3}\,\,;\,\,\,\cot B = \frac{3}{7}\\\sin C = \frac{3}{{\sqrt {10} }}\,\,;\,\,\cos C = \frac{7}{{\sqrt {10} }}\,\,;\,\,\tan C = \frac{3}{7}\,\,;\,\,\cot C = \frac{7}{3}\end{array}\)
Phương pháp giải:
Sử dụng định lý Pi-ta-go để tính cạnh BC.
Cho \(\angle B + \angle C = {90^0}.\) Khi đó ta có: \(\left\{ \begin{array}{l}\sin B = \cos C\\\cos B = \sin C\\\tan B = \cot C\\\cot B = \tan C.\end{array} \right.\)
Lời giải chi tiết:
Áp dụng định lý Pitago cho \(\Delta ABC\) vuông tại \(A\) có : \(A{B^2} + A{C^2} = B{C^2}\)
\( \Leftrightarrow B{C^2} = {7^2} + {21^2} = 490\)\( \Rightarrow BC = 7\sqrt {10} \,\,\,cm.\)
Trong \(\Delta ABC\) vuông tại \(A\) ta có:
\(\sin B = \frac{{AC}}{{BC}} = \frac{{21}}{{7\sqrt {10} }} = \frac{3}{{\sqrt {10} }}\)
\(\cos B = \frac{{AB}}{{BC}} = \frac{7}{{7\sqrt {10} }} = \frac{1}{{\sqrt {10} }}\)
\(\tan B = \frac{{AC}}{{AB}} = \frac{{21}}{7} = 3\)
\(\cot B = \frac{{AB}}{{AC}} = \frac{7}{{21}} = \frac{1}{3}\)
Vì \(\angle B + \angle C = {90^0}\)
\(\begin{array}{l} \Rightarrow \sin C = \cos B = \frac{1}{{\sqrt {10} }}\\\cos C = \sin B = \frac{3}{{\sqrt {10} }}\\\tan C = \cot B = \frac{1}{3}\\\cot C = \tan B = 3\end{array}\)
Chọn A.