Phương pháp giải:

- Trong (ABC) kẻ $GE\parallel BC\,\,\left( {E \in AC} \right)$. Chứng minh $AC \bot \left( {SGE} \right)$.

- Trong (SGE) kẻ $GH \bot SE$ $\left( {H \in SE} \right)$, chứng minh $GH \bot \left( {SAC} \right)$.

- Sử dụng hệ thức lượng trong tam giác vuông để tính khoảng cách.

Lời giải chi tiết:

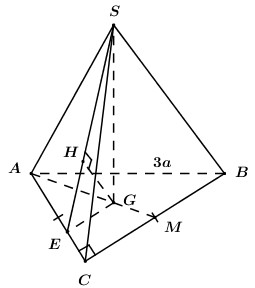
+ Trong (ABC) kẻ $GE\parallel BC\,\,\left( {E \in AC} \right)$.

+ $\left\{ \begin{array}{l}GE\parallel BC\\AC \bot BC\,\,\left( {gt} \right)\end{array} \right. \Rightarrow GE \bot AC$.

+ $\left\{ \begin{array}{l}AC \bot GE\\AC \bot SG\,\,\left( {SG \bot \left( {ABC} \right)} \right)\end{array} \right.$ $\Rightarrow AC \bot \left( {SGE} \right)$.

Trong (SGE) kẻ $GH \bot SE\,\,\left( {H \in SE} \right)$.

+ $\left\{ \begin{array}{l}GH \bot SE\\GH \bot AC\,\,\left( {AC \bot \left( {SGE} \right)} \right)\end{array} \right.$ $\Rightarrow GH \bot \left( {SAC} \right)$.

$\Rightarrow {d_{\left[ {G;\left( {SAC} \right)} \right]}} = GH$.

+ Tam giác ABC vuông cân tại C có AB = 3a $\Rightarrow AC = BC = \dfrac{{AB}}{{\sqrt 2 }} = \dfrac{{3a}}{{\sqrt 2 }}$.

Gọi M là trung điểm của BC. Áp dụng định lí Ta-lét:

$\dfrac{{GE}}{{MC}} = \dfrac{{AG}}{{AM}} = \dfrac{2}{3}$ $\Rightarrow GE = \dfrac{2}{3}MC = \dfrac{2}{3}.\dfrac{{3a}}{{2\sqrt 2 }} = \dfrac{{a\sqrt 2 }}{2}$.

+ $\Delta SGE$: $GH = \dfrac{{SG.GE}}{{\sqrt {S{G^2} + G{E^2}} }} = \dfrac{{a.\dfrac{{a\sqrt 2 }}{2}}}{{\sqrt {{a^2} + \dfrac{{{a^2}}}{2}} }} = \dfrac{{a\sqrt 3 }}{3}$.

Vậy ${d_{\left[ {G;\left( {SAC} \right)} \right]}} = \dfrac{{a\sqrt 3 }}{3}$.