Phương pháp giải:

- Sử dụng định lí: Góc giữa hai đường thẳng chéo nhau là góc giữa đường thẳng này và mặt phẳng song song với nó chứa đường thẳng kia.

- Dựng hình bình hành ABCD, chứng minh $d\left( {SA;BC} \right) = d\left( {B;\left( {SAD} \right)} \right)$.

- Đổi điểm tính khoảng từ H đến (SAD), sử dụng phương pháp dựng 3 nét.

- Xác định góc giữa đường và mặt là góc giữa đường thẳng và hình chiếu của đường thẳng trên mặt phẳng đó.

- Sử dụng tỉ số lượng giác của góc nhọn và hệ thức lượng trong tam giác vuông để tính khoảng cách.

Lời giải chi tiết:

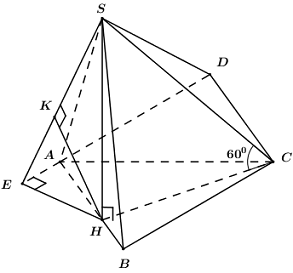
Dựng hình bình hành ABCD, ta có AD // BC nên $BC\parallel \left( {SAD} \right) \supset SA$.

$\Rightarrow d\left( {SA;BC} \right) = d\left( {BC;\left( {SAD} \right)} \right) = d\left( {B;\left( {SAD} \right)} \right)$.

Ta có: $BH \cap \left( {SAD} \right) = A \Rightarrow \dfrac{{d\left( {B;\left( {SAD} \right)} \right)}}{{d\left( {H;\left( {SAD} \right)} \right)}} = \dfrac{{BA}}{{HA}} = \dfrac{3}{2}$ $\Rightarrow d\left( {B;\left( {SAD} \right)} \right) = \dfrac{3}{2}d\left( {H;\left( {SAD} \right)} \right)$.

Trong (ABCD) kẻ $EH \bot AD$ (do $\Delta ABC$ đều nên $\angle ABC = {60^0} \Rightarrow \angle BAD = {120^0}$, do đó điểm E nằm ngoài đoạn thẳng AD về phía A).

Trong (SHE) kẻ $HK \bot SE\,\,\left( {K \in SE} \right)$.

Ta có:

$\begin{array}{l}\left\{ \begin{array}{l}AD \bot HE\\AD \bot SH\end{array} \right. \Rightarrow AD \bot \left( {SHE} \right) \Rightarrow AD \bot HK\\\left\{ \begin{array}{l}HK \bot SD\\HK \bot SE\end{array} \right. \Rightarrow HK \bot \left( {SAD} \right)\\ \Rightarrow d\left( {H;\left( {SAD} \right)} \right) = HK\end{array}$

Vì $\angle BAD = {120^0} \Rightarrow \angle HAE = {60^0}$.

Xét $\Delta AHE$ vuông tại E có $HE = AH.\sin {60^0} = \dfrac{2}{3}AB.\dfrac{{\sqrt 3 }}{2} = \dfrac{{\sqrt 3 }}{3}.2a = \dfrac{{2a\sqrt 3 }}{3}$.

Ta có: $SH \bot \left( {ABC} \right)$ nên HC là hình chiếu của SC lên (ABC) $\Rightarrow \angle \left( {SC;\left( {ABC} \right)} \right) = \angle \left( {SC;HC} \right) = \angle SCH = {60^0}$.

Áp dụng định lí Co-sin trong tam giác AHC ta có:

$\begin{array}{l}H{C^2} = A{H^2} + A{C^2} - 2.AH.AC.\cos \angle HAC\\H{C^2} = {\left( {\dfrac{2}{3}.2a} \right)^2} + {\left( {2a} \right)^2} - 2.\left( {\dfrac{2}{3}.2a} \right).2a.\cos {60^0}\\H{C^2} = \dfrac{{28{a^2}}}{9} \Rightarrow HC = \dfrac{{2a\sqrt 7 }}{3}\end{array}$

Xét tam giác vuông SHC có: $SH = HC.tan{60^0} = \dfrac{{2a\sqrt 7 }}{3}.\sqrt 3  = \dfrac{{2a\sqrt {21} }}{3}$.

Áp dụng hệ thức lượng trong tam giác vuông SHE có:

$HK = \dfrac{{SH.HE}}{{\sqrt {S{H^2} + H{E^2}} }} = \dfrac{{\dfrac{{2a\sqrt {21} }}{3}.\dfrac{{2a\sqrt 3 }}{3}}}{{\sqrt {{{\left( {\dfrac{{2a\sqrt {21} }}{3}} \right)}^2} + {{\left( {\dfrac{{2a\sqrt 3 }}{3}} \right)}^2}} }} = \dfrac{{a\sqrt {42} }}{6}$.

Vậy $d\left( {SA;BC} \right) = \dfrac{3}{2}HK = \dfrac{{a\sqrt {42} }}{4}$.

Chọn D.