Phương pháp giải:

- Sử dụng định lí: Hai mặt phẳng cùng vuông góc với mặt phẳng thứ ba thì giao tuyến của chúng sẽ vuông góc với mặt phẳng thứ ba đó để chứng minh $SI \bot \left( {ABCD} \right)$.

- Đổi về bài toán tính khoảng cách từ chân đường cao đến mặt phẳng (SBC).

- Tìm góc giữa mặt phẳng $\left( {SBC} \right);\left( {ABCD} \right)$: Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và cùng vuông góc với giao tuyến.

- Áp dụng tỉ số lượng giác của góc nhọn trong tam giác vuông để tính khoảng cách.

Lời giải chi tiết:

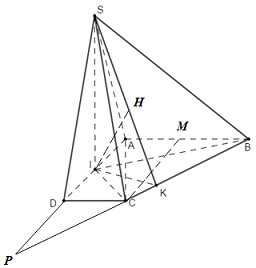
Ta có $\left\{ \begin{array}{l}\left( {SBI} \right) \bot \left( {ABC{\rm{D}}} \right)\\\left( {SIC} \right) \bot \left( {ABC{\rm{D}}} \right)\\\left( {SIB} \right) \cap \left( {SIC} \right) = SI\end{array} \right. \Rightarrow SI \bot \left( {ABC{\rm{D}}} \right)$

Trong (ABCD) kéo dài DI cắt BC tại P, khi đó ta có $DI \cap \left( {SBC} \right) = P$.

Áp dụng định lí Ta-lét ta có: $\dfrac{{PD}}{{PA}} = \dfrac{{CD}}{{AB}} = \dfrac{a}{{2a}} = \dfrac{1}{2}$ $\Rightarrow D$ là trung điểm của AP.

$\Rightarrow DP = AD = 2a,\,\,IP = ID + DP = a + 2a = 3a$.

$\begin{array}{l} \Rightarrow \dfrac{{DP}}{{IP}} = \dfrac{{2a}}{{3a}} = \dfrac{2}{3}\\ \Rightarrow \dfrac{{d\left( {D;\left( {SBC} \right)} \right)}}{{d\left( {I;\left( {SBC} \right)} \right)}} = \dfrac{{DP}}{{IP}} = \dfrac{2}{3}\\ \Rightarrow d\left( {D;\left( {SBC} \right)} \right) = \dfrac{2}{3}d\left( {I;\left( {SBC} \right)} \right).\end{array}$

Trong (ABCD) kẻ $IK \bot BC\,\,\left( {K \in BC} \right)$, trong (SIK) kẻ $IH \bot SK\,\,\left( {H \in SK} \right)$ ta có:

$\begin{array}{l}\left\{ \begin{array}{l}BC \bot SI\\BC \bot IK\end{array} \right. \Rightarrow BC \bot \left( {SIK} \right) \Rightarrow BC \bot IH\\\left\{ \begin{array}{l}IH \bot BC\\IH \bot SK\end{array} \right. \Rightarrow IH \bot \left( {SBC} \right) \Rightarrow d\left( {I;\left( {SBC} \right)} \right) = IH\end{array}$

Ta có hình thang ABCD vuông tại A và D có $ID = IA = \dfrac{{AD}}{2} = a;$ $DC = a;$ $AB = 2a$.

Áp dụng định lí Pytago ta có:

$\begin{array}{l}IC = \sqrt {I{D^2} + C{D^2}}  = \sqrt {{a^2} + {a^2}}  = a\sqrt 2 \\IB = \sqrt {I{A^2} + A{B^2}}  = \sqrt {{a^2} + 4{a^2}}  = a\sqrt 5 \end{array}$

Kẻ $CM \bot AB$ ta có: AMCD là hình chữ nhật nên $CM = AD = 2a$, $MB = AB - AM = 2a - a = a$.

Áp dụng định lí Pytago trong tam giác vuông BCM có: $BC = \sqrt {B{M^2} + C{M^2}}  = \sqrt {{a^2} + 4{a^2}}  = a\sqrt 5$.

Trong (ABCD) kẻ $IK \bot BC\,\,\left( {K \in BC} \right)$ ta có:

$\begin{array}{l}{S_{BIC}} = \dfrac{1}{2}IK.BC = {S_{ABCD}} - {S_{DIC}} - {S_{ABI}}\\\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{2}.AD.\left( {AB + CD} \right) - \dfrac{1}{2}ID.CD - \dfrac{1}{2}IA.AB\\\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{2}.2a.\left( {2a + a} \right) - \dfrac{1}{2}.a.a - \dfrac{1}{2}.a.2a\\\,\,\,\,\,\,\,\,\,\, = 3{a^2} - \dfrac{1}{2}{a^2} - {a^2} = \dfrac{{3{a^2}}}{2}\end{array}$

Lại có

$\begin{array}{l}{S_{BIC}} = \dfrac{1}{2}IK.BC\\ \Rightarrow \dfrac{{3{a^2}}}{2} = \dfrac{1}{2}.IK.a\sqrt 5 \\ \Rightarrow IK = \dfrac{{3a\sqrt 5 }}{5}.\end{array}$

Ta có: $\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABCD} \right) = BC\\SK \subset \left( {SBC} \right),\,\,SK \bot BC\\IK \subset \left( {ABCD} \right),\,\,IK \bot BC\end{array} \right.$ $\Rightarrow \angle \left( {\left( {SBC} \right);\left( {ABCD} \right)} \right) = \angle \left( {SK;IK} \right) = \angle SKI = {60^0}$.

Xét tam giác vuông IHK có: $IH = IK.\sin \angle SKI = \dfrac{{3a\sqrt 5 }}{5}.\dfrac{{\sqrt 3 }}{2} = \dfrac{{3a\sqrt {15} }}{{10}}$.

Vậy $d\left( {D;\left( {SBC} \right)} \right) = \dfrac{2}{3}d\left( {I;\left( {SBC} \right)} \right) = \dfrac{2}{3}IH = \dfrac{{a\sqrt {15} }}{5}.$

Chọn A.