Câu hỏi:
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác cân tại \(B\), cạnh bên \(SA\) vuông góc với đáy, \(I\) là trung điểm \(AC\). Khẳng định nào sau đây sai?
- A \(\left( {SAB} \right) \bot \left( {ABC} \right)\)
- B \(\left( {SAC} \right) \bot \left( {SAB} \right)\)
- C \(\left( {SAC} \right) \bot \left( {ABC} \right)\)
- D \(\left( {SBI} \right) \bot \left( {SAC} \right)\)
Phương pháp giải:
Sử dụng định lí: Hai mặt phẳng vuông góc với nhau khi và chỉ khi: Mặt phẳng này chứa đường thẳng vuông góc với mặt phẳng kia.
Lời giải chi tiết:
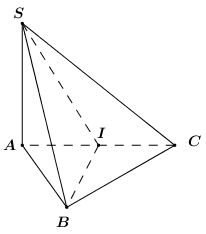
Vì \(\left\{ \begin{array}{l}SA \bot \left( {ABC} \right)\\SA \subset \left( {SAB} \right)\\SA \subset \left( {SAC} \right)\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\left( {SAB} \right) \bot \left( {ABC} \right)\\\left( {SAC} \right) \bot \left( {ABC} \right)\end{array} \right.\) , do đó đáp án A và C đúng.
Tam giác \(ABC\) cân tại \(B\,\,\left( {gt} \right)\) nên \(BI \bot AC\) (đường trung tuyến đồng thời là đường cao).
Ta có: \(\left\{ \begin{array}{l}BI \bot AC\\BI \bot SA\,\,\,\left( {SA \bot \left( {ABC} \right)} \right)\end{array} \right. \Rightarrow BI \bot \left( {SAC} \right)\).
Mà \(BI \subset \left( {SBI} \right)\), suy ra \(\left( {SBI} \right) \bot \left( {SAC} \right)\), do đó đáp án D đúng.
Vậy khẳng định B sai.
Chọn B.


















